SAT1000 - P941
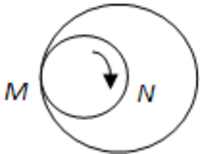 As shown above, a small circle with diameter
is rotating counterclockwise along the interior side of the big circle with diameter
without slipping,
and
are two endpoints of a diameter of the small circle.
As shown above, a small circle with diameter
is rotating counterclockwise along the interior side of the big circle with diameter
without slipping,
and
are two endpoints of a diameter of the small circle.
Then as it is rotating, which of the following is the locus of points and ?
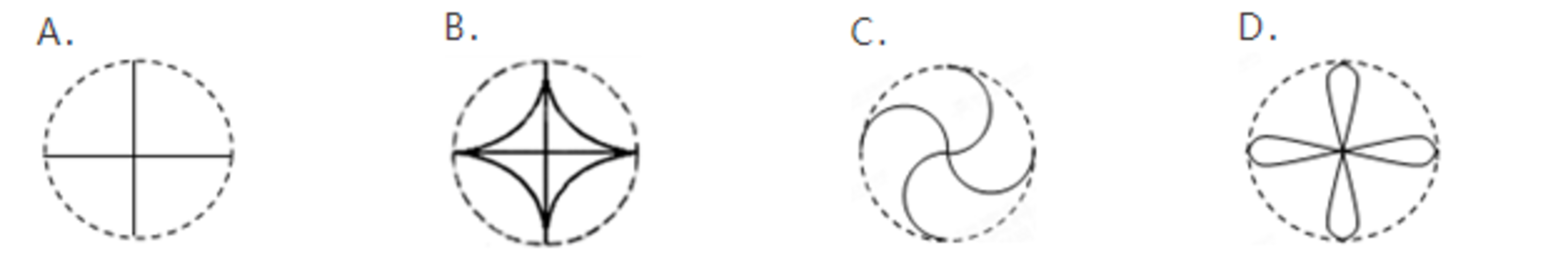
Have a look at my problem set: SAT 1000 problems
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
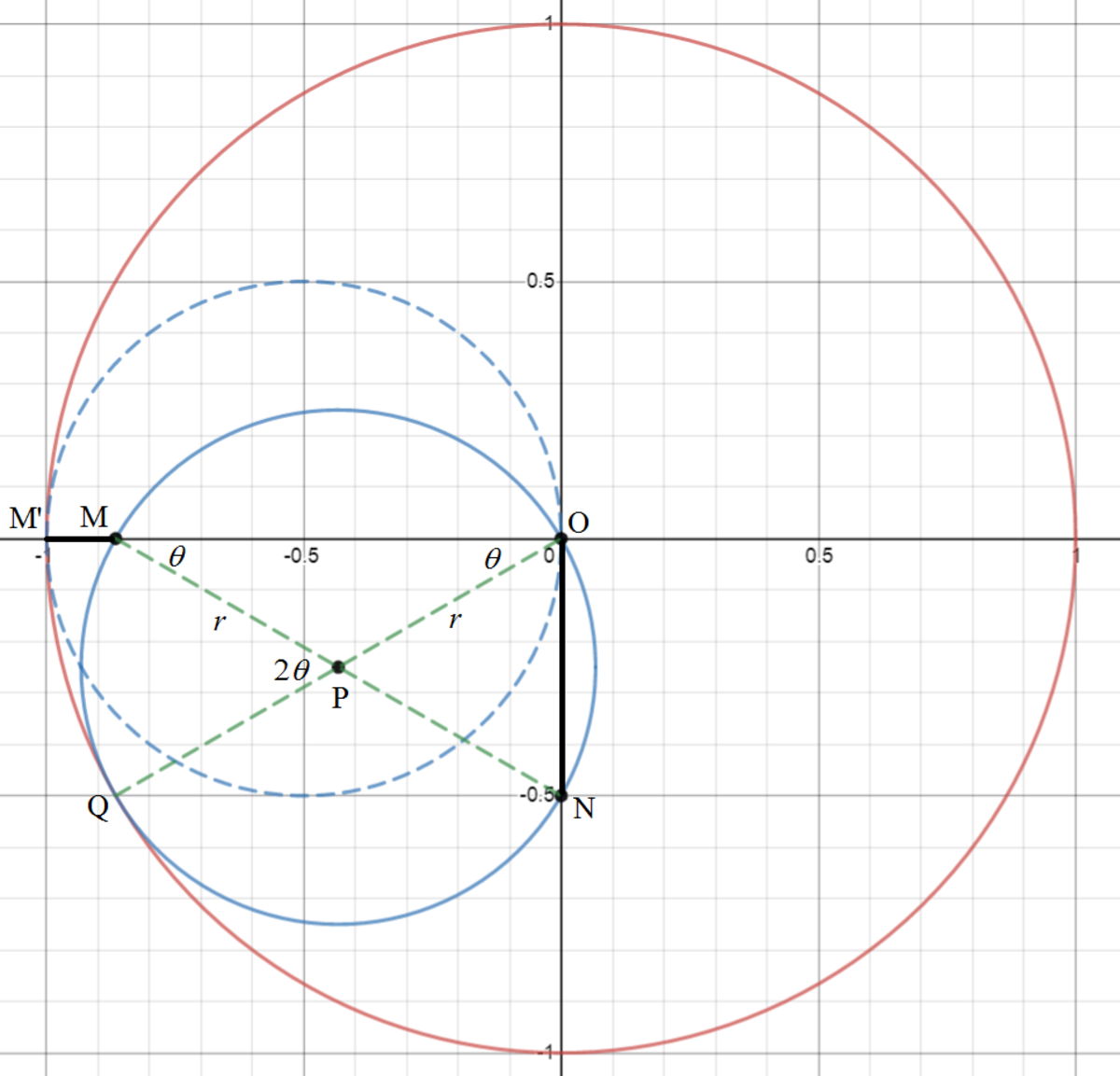
This is known as a Tusi couple , and the following animation (courtesy of Wikipedia) shows the locus of points for N :
By symmetry, M will be the locus of points perpendicular to the locus of points for N , making the answer A .