SAT Midpoint Formula
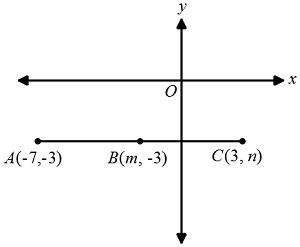 In the figure above, point
is the midpoint of segment
. What is the value of
In the figure above, point
is the midpoint of segment
. What is the value of
(A)
(B)
(C)
(D)
(E)
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Correct Answer: D
Solution 1:
Since points A , B , and C are collinear, they have the same y − coordinate, -3. Therefore, n = − 3 .
We can find the length of A C by subtracting the x − coordinates of points A and C .
A C = 3 − ( − 7 ) = 3 + 7 = 1 0 .
By definition, the midpoint B lies halfway between A and C . Therefore, it is located 5 units to the right of point A , and 5 units to the left of point C . We add 5 to the x − coordinate of point A , or subtract 5 from the x − coordinate of point C to find that point C is located at ( − 2 , − 3 ) . So, m = − 2 .
We can now find m − n , which is − 2 − ( − 3 ) = − 2 + 3 = 1 .
Solution 2:
Tip: Midpoint formula: M = ( 2 x 1 + x 2 , 2 y 1 + y 2 ) .
As in Solution 1, we find that since points A , B , and C are collinear, they have the same y − coordinate, -3, and that therefore n = − 3 .
Now that we know that A = ( − 7 , − 3 ) and C = ( 3 , − 3 ) , we use the midpoint formula to find the coordinates of point B .
B B B = ( 2 − 7 + 3 , 2 − 3 + ( − 3 ) ) = ( 2 − 4 , 2 − 6 ) = ( − 2 , − 3 )
Therefore, m = − 2 and m − n = − 2 − ( − 3 ) = − 2 + 3 = 1 .
Incorrect Choices:
(A)
Tip: Read the entire question carefully.
Tip: When distributing, be careful with signs!
If you solve for m + n , instead of for m − n , you will get this wrong answer. Or, if you forget to distribute the negative sign when subtracting n from m , like this
m − n = − 2 - ( − 3 ) = − 2 - 3 = − 5 ,
you will get this wrong answer.
(B)
Tip: Read the entire question carefully.
If you solve for n , instead of for m − n , you will get this wrong answer.
(C)
Tip: Read the entire question carefully.
If you solve for m , instead of for m − n , you will get this wrong answer.
(E)
This wrong choice is just meant to confuse you.