Save the rod
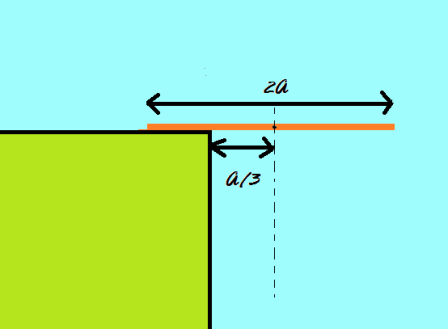 A rod of mass
and length
is placed horizontally on the edge of a table. Initially, the centre of mass of the rod is at a distance of
from the edge. The rod is released from the rest. The rod slips after it has turned through an angle
.
The coefficient of friction
between the rod and the table can be expressed as
Find
A rod of mass
and length
is placed horizontally on the edge of a table. Initially, the centre of mass of the rod is at a distance of
from the edge. The rod is released from the rest. The rod slips after it has turned through an angle
.
The coefficient of friction
between the rod and the table can be expressed as
Find
Note
- and are positive, co-prime integers.
- Liked it? Go here for more.
The answer is 3.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Initially the rod rotates about the edge. Using principle of conservation of energy , 0 + 0 = 2 1 I ω 2 + ( − M g 3 a sin θ ) . . . . . ( 1 ) Where , I = 1 2 M ( 2 a ) 2 + M ( a / 3 ) 2 After putting the value of I in ( 1 ) ,we get ω 2 = 2 a 3 g sin θ . . . . . . . . . . . . . . . . . . . ( 2 ) Diff. wrt. θ ,we get, 2 ω d θ d ω = 2 a 3 g cos θ or ω d θ d ω = 4 a 3 g cos θ . . . . . . . ( 3 ) Since α = d t d ω = d θ d ω × d t d θ = ω d θ d ω Equations for motion are M g cos θ − N = M α ( a / 3 ) = 3 M a ω × d θ d ω Using ( 3 ) we get N = 4 3 × M g cos θ . . . . . . . . . . . . . . . . . . . . . . ( 4 ) Also μ N − M g sin θ = M ( a / 3 ) ω 2 ⇒ μ N − M g sin θ = 3 M a ( 2 a 3 g sin θ ) = 2 M g sin θ Hence using equation ( 4 ) we get μ = 1 2 tan θ