SCAA Logo
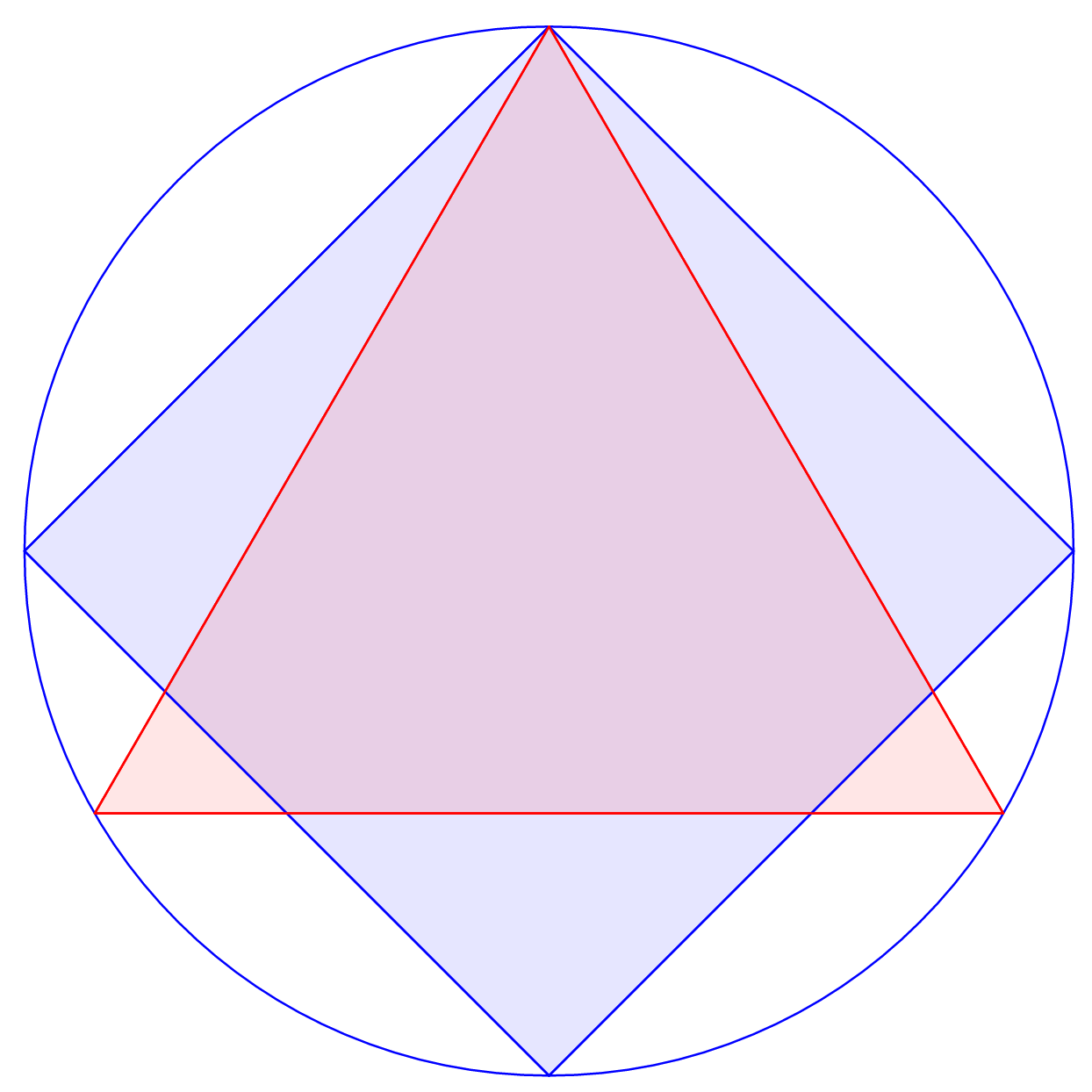
The figure shows a unit circle with a square and an equilateral triangle inscribed in it.
The square and equilateral triangle share a vertex.
The overlapping area of the square and triangle can be expressed as a b + d c , where a , b , c and d are integers with b square-free and c , d coprime.
Find a b + c d .
The answer is -30.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
10 solutions
Nice problem and elegant solution! Upvoted (+1)! I could only think of bashing it using coordinate geometry.
Nice question! Who knew such a simple diagram could require so much calculation?
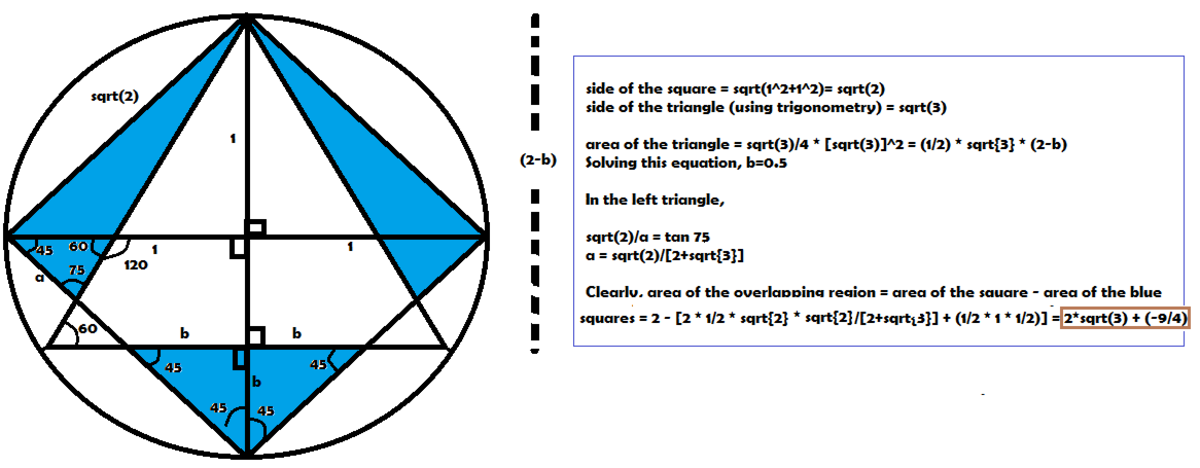
Area of square = As = 2
Area of lateral triangle = At = 2 1 2 × 2 tan 1 5 = 2 − 3
Area of bottom triangle = Ab = 2 1 × 2 1 × 1 = 4 1
Overlapping area = As - Ab - 2At = 2 − 4 1 − 2 ( 2 − 3 ) = 2 3 − 4 9
So ab + cd = (2)(3) + (-4)(9) = -30
Nice and simple solution!
What a coincident !! Absolutely the same method . Ujjwal, I do not know how to sent massage to you. @https://brilliant.org/profile/ujjwal-ulesb8/
Log in to reply
So good to hear from you sir! Glad I got the notification for this message. But sometimes messages go unannounced and hence unnoticed. So do please send an email to be sure.
The same solution has been posted above by my friend vishwash but the solution is not easy to read as it has small letters so i have posted the same solution here with large letters .
I try to solve this using Analytic Geometry, also known as Coordinate Geometry.
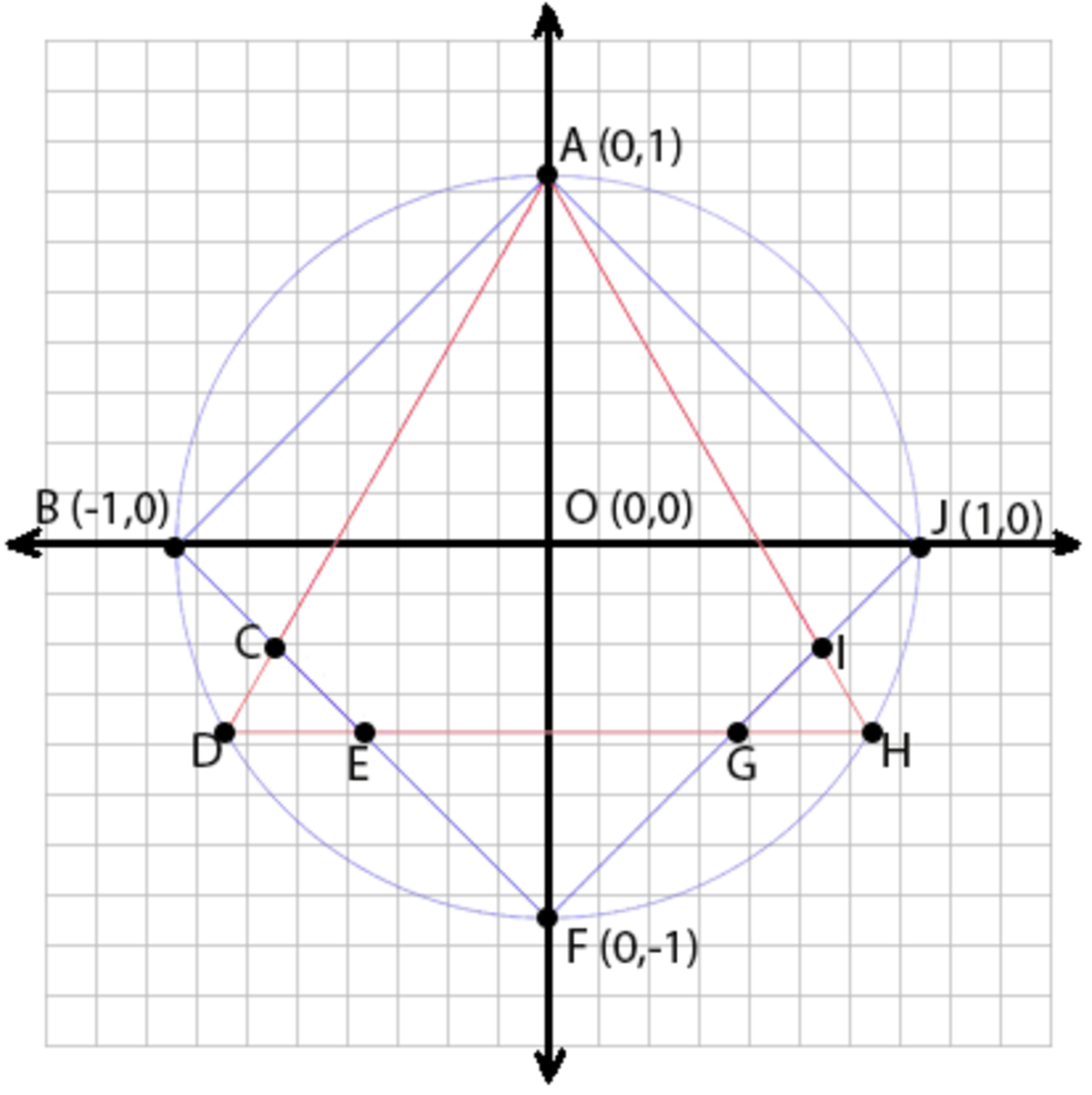
Let the center point of the circle is ( 0 , 0 ) and satisfy the equation x 2 + y 2 = 1 . To find the area of polygon A C E G I we need to find the coordinate of point A , C , E , G and I .
From the picture above we see that the coordinate of point A is ( 0 , 1 ) .
First, find the equation of line D H , A D , A H , B F a n d F J . .
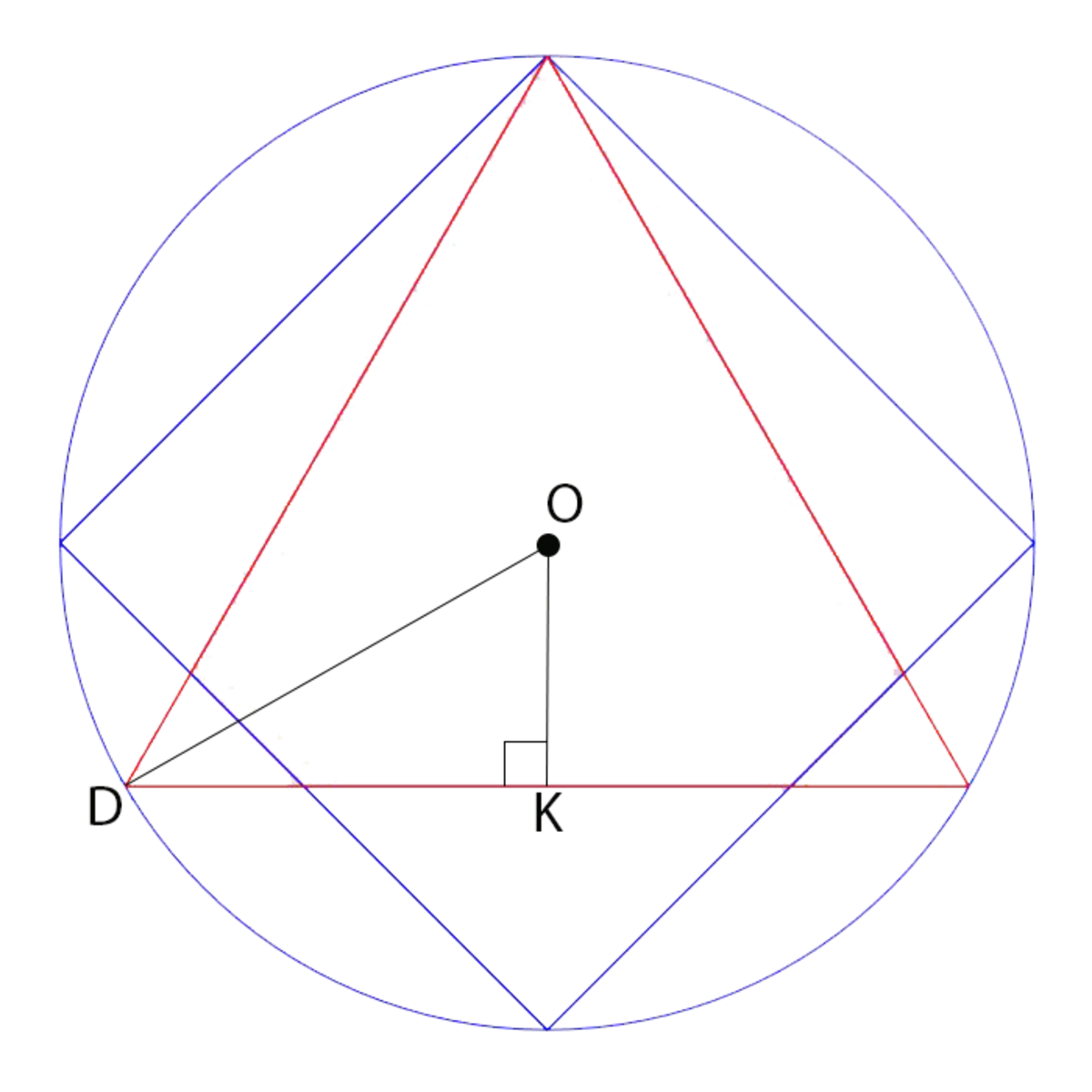
Since O D = 1 , ∠ O D K = 3 0 ∘ , and sin 3 0 ∘ = 0 . 5 , we know that O K = 0 . 5 .
So, the equation of line D H is y = − 0 . 5 .
Take y = − 0 . 5 and substitute to x 2 + y 2 = 1 , we found that point D ( − 0 . 5 3 , − 0 . 5 ) and H ( 0 . 5 3 , − 0 . 5 ) .
From A ( 0 , 1 ) and D ( − 0 . 5 3 , − 0 . 5 ) , equation of line A D is y = 3 x + 1 .
From A ( 0 , 1 ) and H ( 0 . 5 3 , − 0 . 5 ) , equation of line A H is y = − 3 x + 1 .
From B ( − 1 , 0 ) and F ( 0 , − 1 ) , equation of line B F is y = − x − 1 .
From J ( 1 , 0 ) and F ( 0 , − 1 ) , equation of line F J is y = x − 1 .
The intersection of line A D and B F produce point C ( − 3 + 1 , 3 − 2 ) .
The intersection of line B F and D H produce point E ( − 5 , − 5 ) .
The intersection of line D H and F J produce point G ( 5 , − 5 ) .
The intersection of line A H and F J produce point I ( 3 − 1 , 3 − 2 ) .
Using the method Area of Irregular Polygon - Coordinate Geometry by using coordinate of point A , C , E , G , and I .
So, we found that the area of polygon A C E G I which is the overlapping area of square and triangle is
Overlapping Area = ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ 0 3 − 1 0 . 5 − 0 . 5 − 3 + 1 0 1 3 − 2 − 0 . 5 − 0 . 5 3 − 2 1 1 1 1 1 1 1 ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣
Overlapping Area = 2 3 − 4 9 .
Answer: a b + c d = 2 ⋅ 3 + ( − 9 ) ⋅ 4 = -30 .
thought someone would do it this way but it's too complicated for me :)
messed up with coordinates nice job
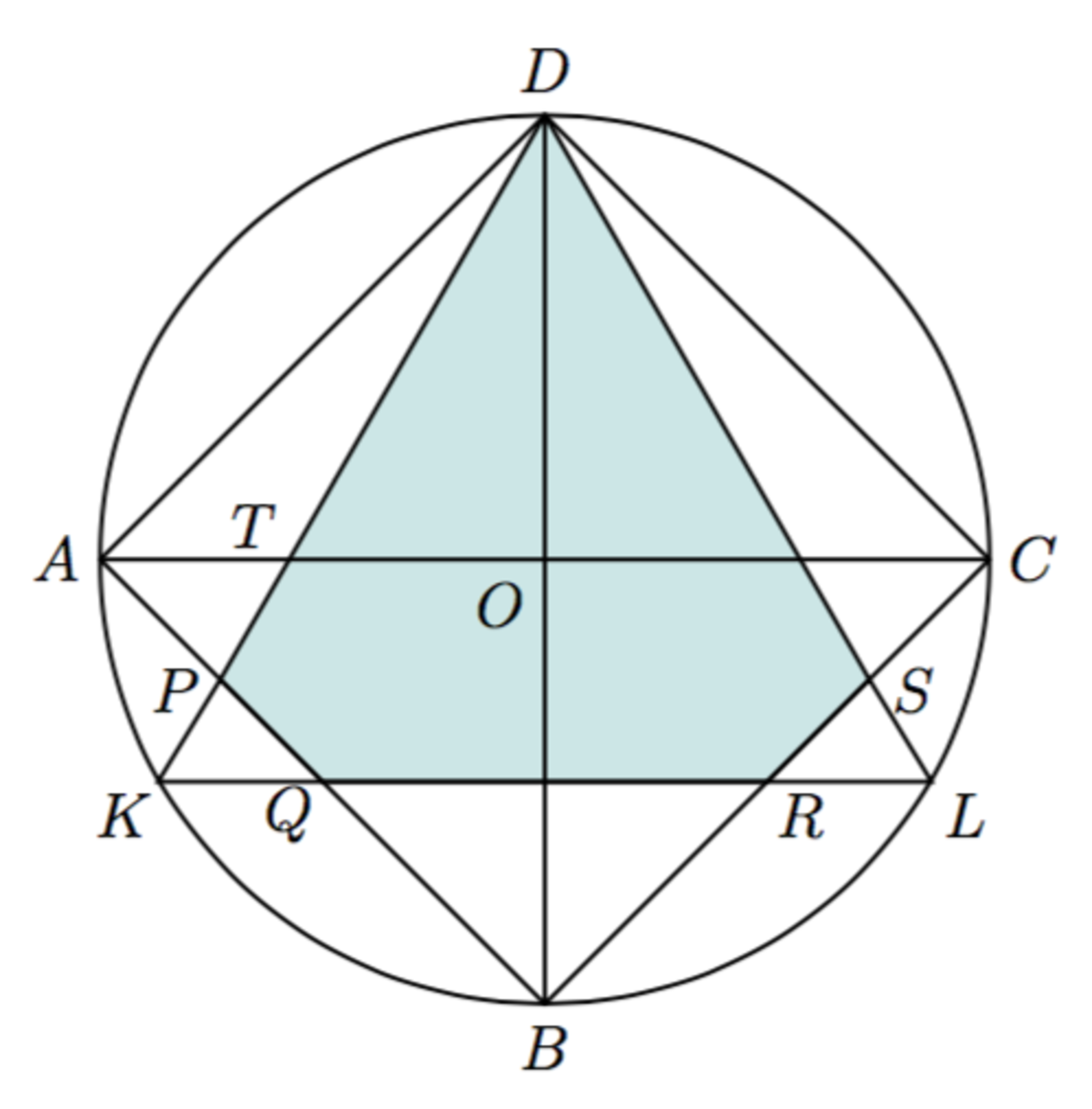
There are two main approaches to this problem.
Consider the Square and take away from the areas of the three triangles that do not overlap. Ujjwal Rane and Lolly Lau has done it below.
Second approach to take away from the areas of the equilateral triangle, the areas of the two identical triangles not overlapping. There are three diffrent solutions for this given below as of to day. I add the fourth below.
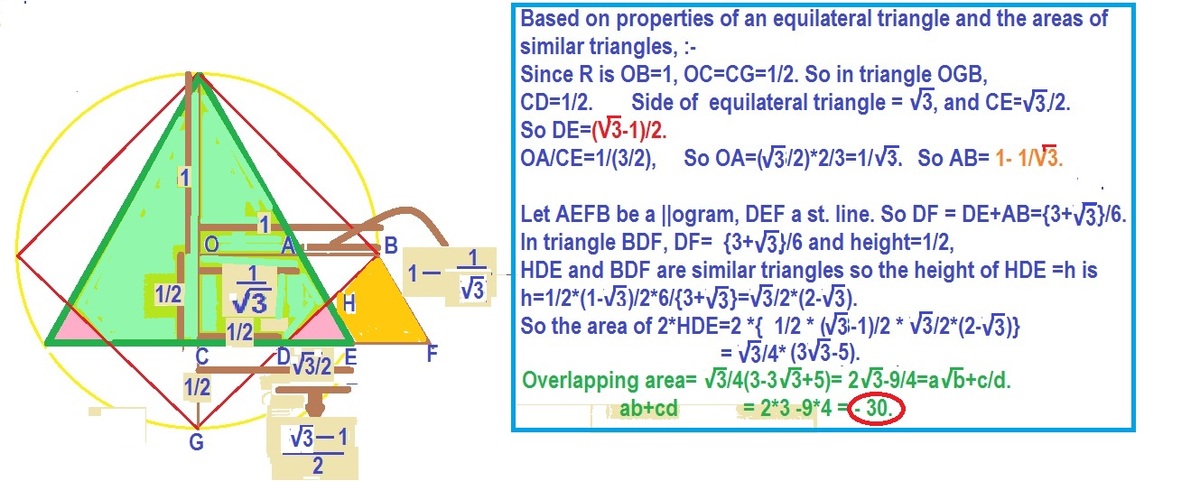
This is a more detailed version of @Lolly Lau 's Solution 2
First of all, we need to find the lengths of the square and the triangle. Refer to the diagram below (ignore the A at the bottom left)
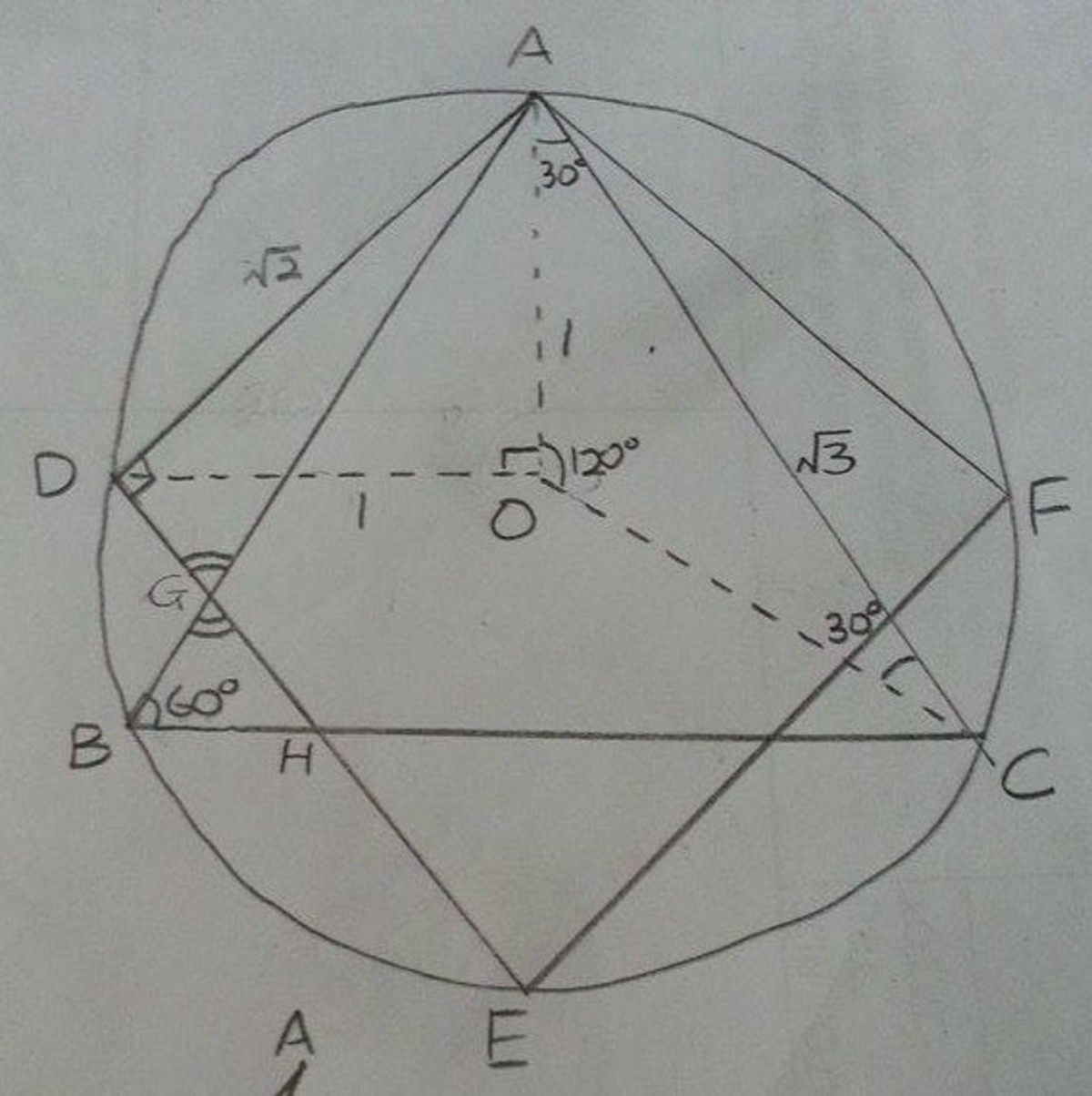
Remember, a unit circle has a radius of 1 .
First, notice that A O and D O are the radius of the circle and the diagonals of the square A D E F . These two lines form a right angle at O , and we can use Pythagoras' Theorem to find the side of the square:
A D = D O 2 + A O 2 = 1 2 + 1 2 = 2
Next, notice that A O and C O are the angle bisectors of ∠ B A C and ∠ B C A respectively. This implies that ∠ O A C = ∠ O C A = 3 0 ∘ . Therefore, ∠ A O C = 1 2 0 ∘ , and we can use sine rule to find the side of the triangle:
sin ∠ A O C A C = sin ∠ O A C O C ⟹ A C = sin 3 0 ∘ 1 × sin 1 2 0 ∘ = 2 3 ÷ 2 1 = 3
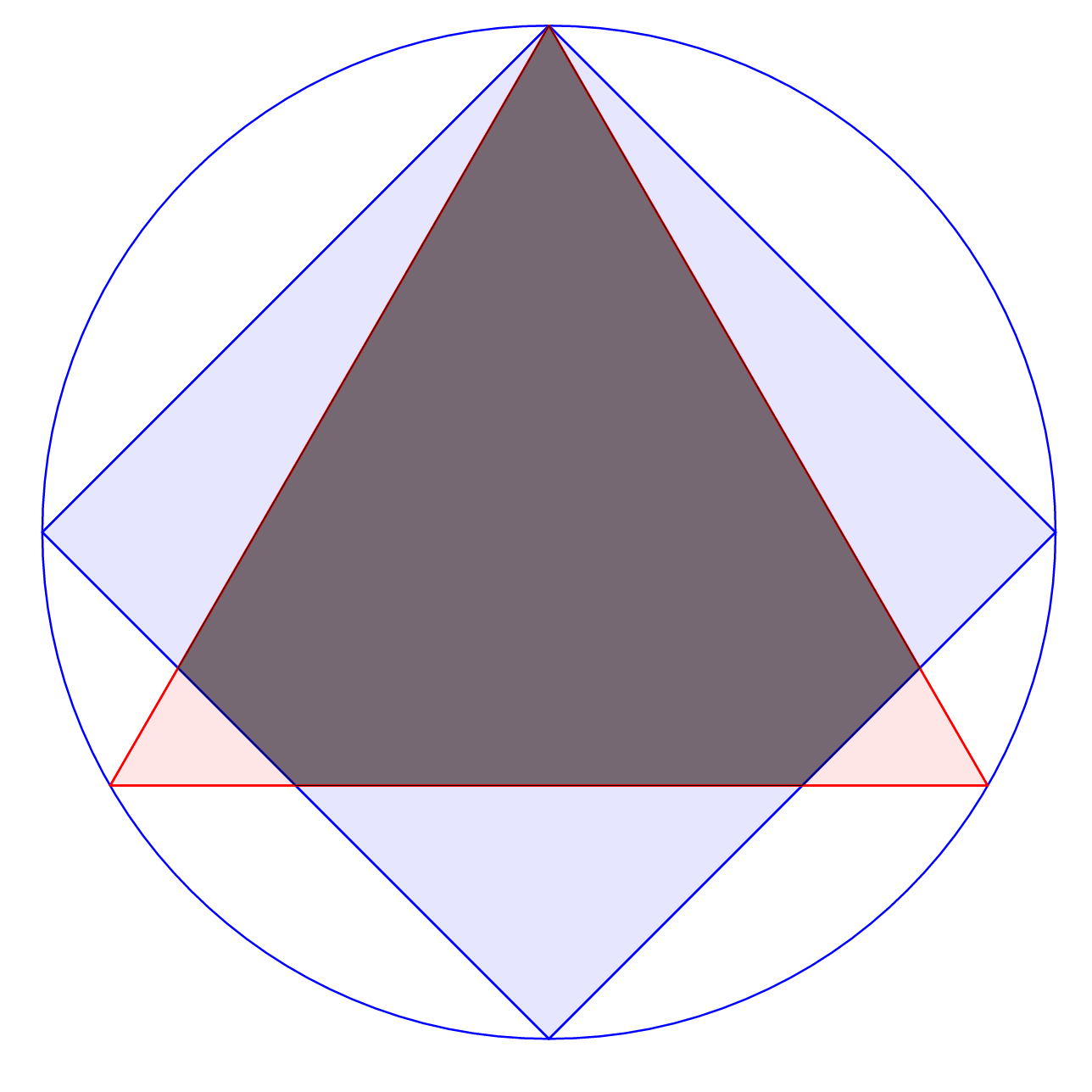
Now, to find the overlapping area, we can calculate the area of the equilateral triangle, and subtract the two small red triangles (one of them is labelled as △ B G H in the diagram)
Overlapping area = Area of △ A B C − 2 × Area of △ B G H
Finding the area of △ A B C is easy:
Area of △ A B C = 2 1 ( 3 ) 2 sin 6 0 ∘ = 2 3 ( 2 3 ) = 4 3 3
Finding the area of △ B G H is NOT easy, but you can do it step by step. First, we will need to find the length of A G :
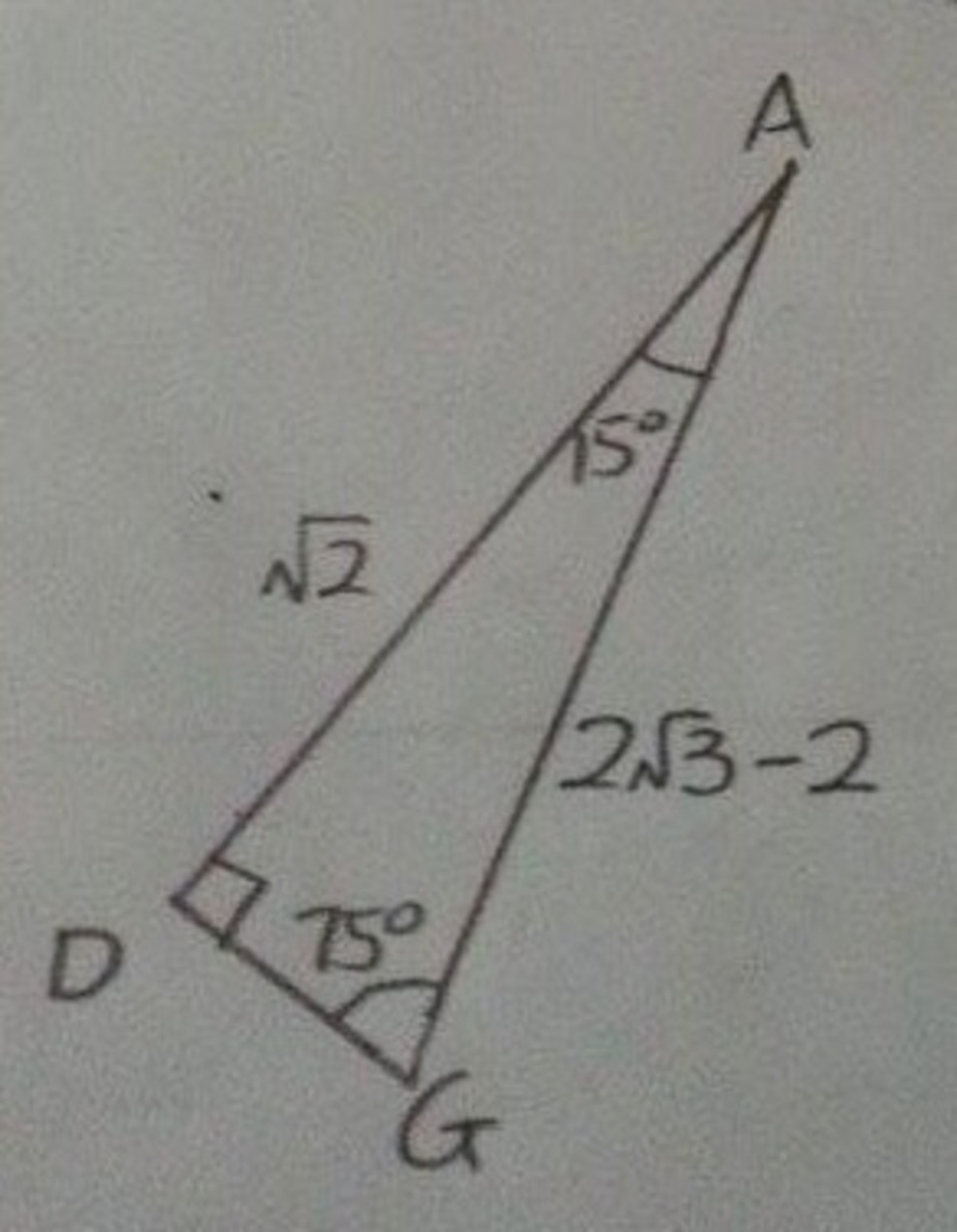
∠ D A G = 2 ∠ D A F − ∠ B A C = 2 9 0 ∘ − 6 0 ∘ = 1 5 ∘
Therefore, ∠ D G A = 7 5 ∘
Using sine rule and the formula for addition of angles , you can find the length of A G in terms of square roots:
sin 7 5 ∘ = ( sin ( 4 5 ∘ + 3 0 ∘ ) ) = ( sin 4 5 ∘ cos 3 0 ∘ + sin 3 0 ∘ cos 4 5 ∘ ) = ( 2 1 × 2 3 + 2 1 × 2 1 ) = 2 2 3 + 1
sin ∠ A D G A G = sin ∠ D G A A D A G = sin 7 5 ∘ 2 sin 9 0 ∘ = 2 2 3 + 1 2 ( 1 ) = 3 + 1 4 = ( 3 + 1 ) ( 3 − 1 ) 4 ( 3 − 1 ) = 2 4 ( 3 − 1 ) = 2 ( 3 − 1 ) = 2 3 − 2
With this, we can calculate the lengths of sides of △ B G H :
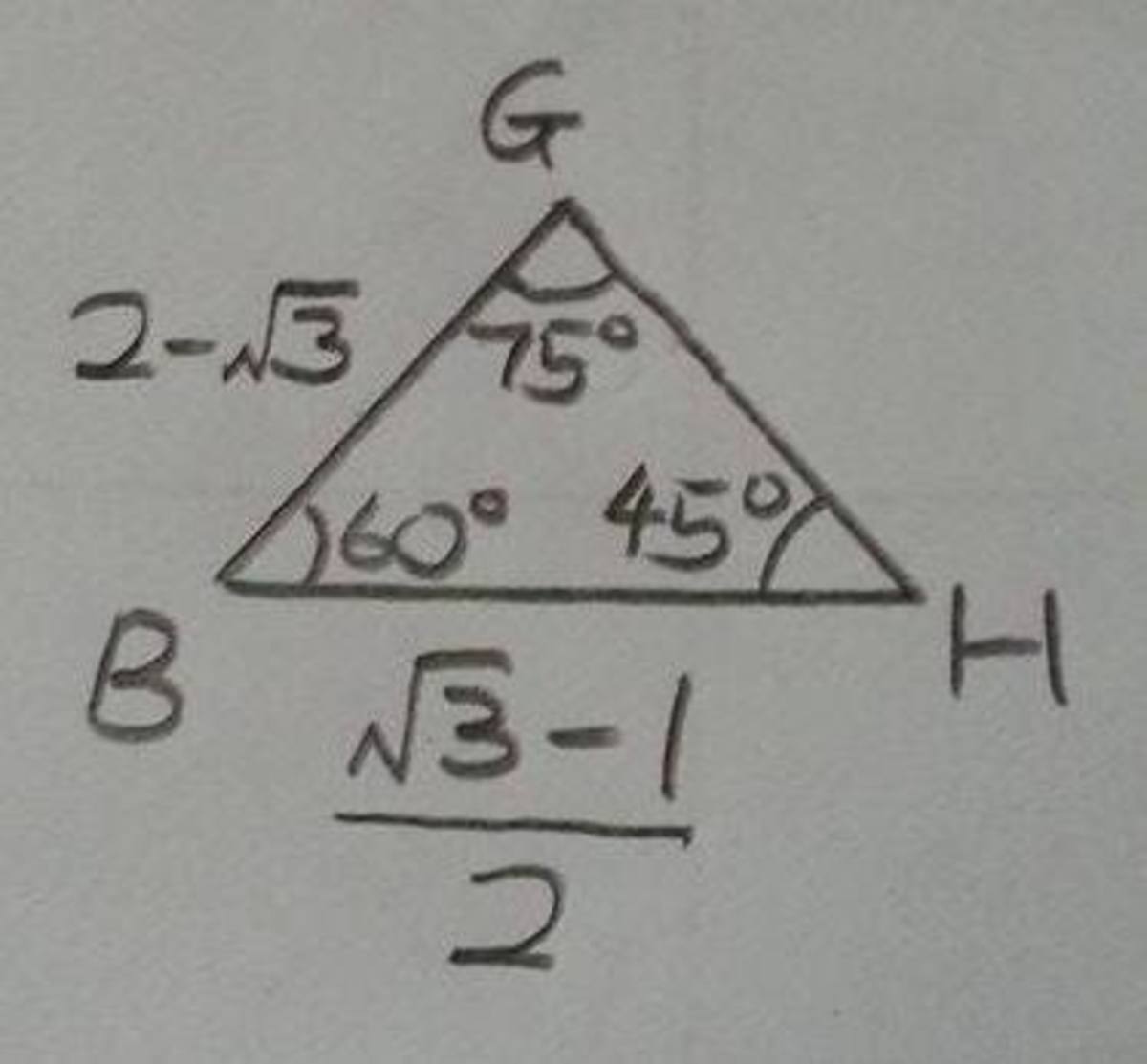
B G = A B − A G = 3 − ( 2 3 − 2 ) = 2 − 3
∠ B G H and ∠ D G A are opposite angles, therefore ∠ B G H = 7 5 ∘ , and ∠ B H G = 4 5 ∘
sin ∠ B G H B H = sin ∠ B H G B G B H = sin 4 5 ∘ ( 2 − 3 ) sin 7 5 ∘ = ( 2 − 3 ) ( 2 2 3 + 1 ) ÷ 2 1 = 2 2 ( 2 − 3 ) ( 3 + 1 ) ( 2 ) = 2 2 3 + 2 − 3 − 3 = 2 3 − 1
Therefore, area of △ B G H = 2 1 ( 2 3 − 1 ) ( 2 − 3 ) sin 6 0 ∘ = 4 2 3 − 2 − 3 + 3 ( 2 3 ) = 8 3 ( 3 3 − 5 ) = 8 9 − 5 3
Overlapping area = Area of △ A B C − 2 × Area of △ B G H
= 4 3 3 − 2 ( 8 9 − 5 3 ) = 4 3 3 − ( 9 − 5 3 ) = 4 8 3 − 9 = 2 3 − 4 9
⟹ a = 2 , b = 3 , c = − 9 , d = 4 , a b + c d = 2 ( 3 ) + ( − 9 ) ( 4 ) = 6 − 3 6 = − 3 0
I did it in the same way!
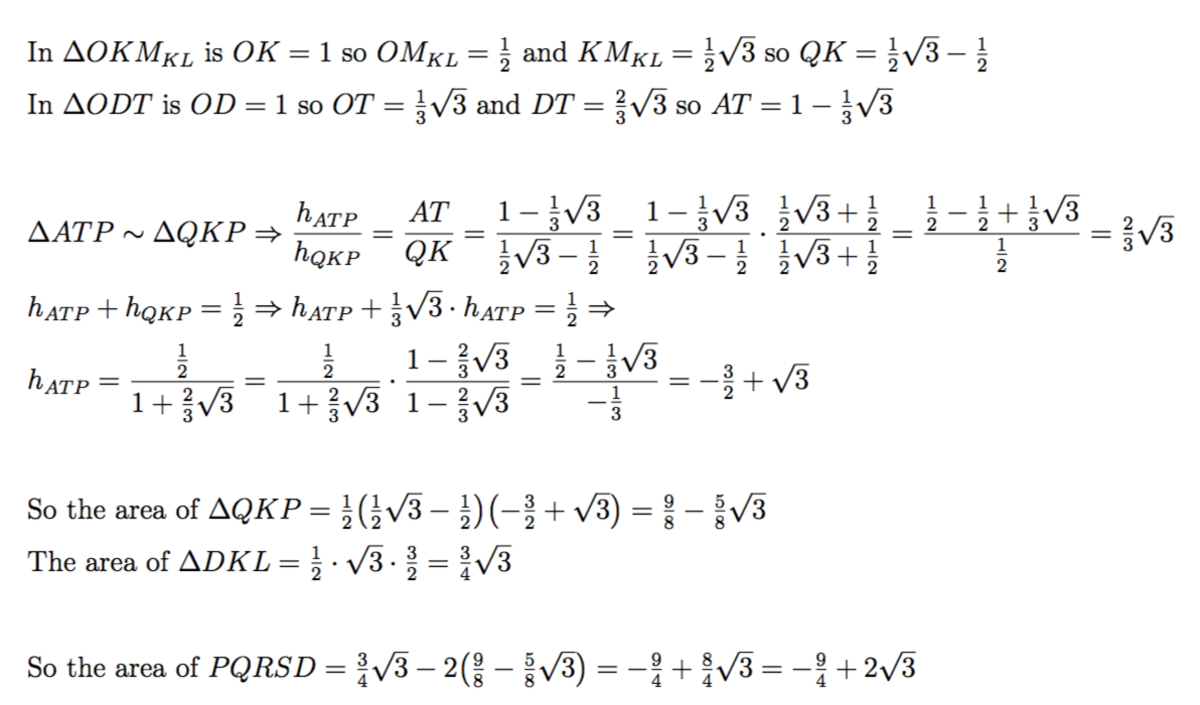
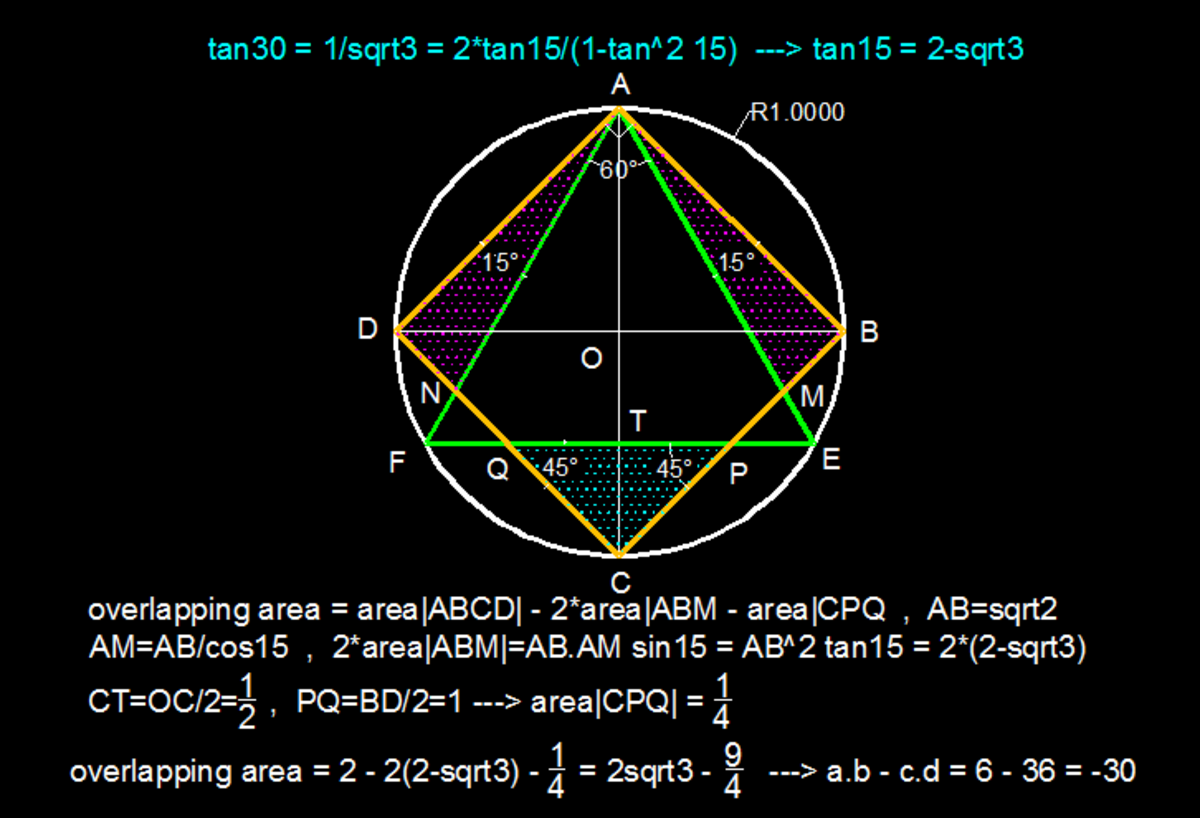
Relevant wiki: Length and Area - Composite Figures - Intermediate
Solution 1
Area of blue triangle at the bottom = quarter of square * length ratio squared * 2 = 2 1 × 1 × ( 1 − sin 6 π ) 2 × 2 = 4 1
Area of triangle = a b sin C = 2 1 a ( sin A a sin B ) sin C = 2 sin A a 2 sin B sin C = 2 sin ( π − B − C ) a 2 sin B sin C = 2 sin ( B + C ) a 2 sin B sin C = 2 ( sin B cos C + cos B sin C ) a 2 sin B sin C = 2 ( cot B + cot C ) a 2
Area of each triangle at the top = 2 ( cot 1 2 π + cot 2 π ) ( 2 ) 2 = 2 − 3
Overlapping area = 2 − 4 1 − ( 2 − 3 ) × 2 = 2 3 − 4 9
Answer = 2 × 3 + ( − 9 ) × 4 = − 3 0
Solution 2
Similarly,
Overlapping area = Area of equilateral triangle - Area of red acute triangle * 2
Area of equilateral triangle = ( 2 1 × 1 × 1 × sin 3 2 π × 3 ) = 4 3 3
Base of each red acute triangle (horizontal side) = 2 1 × sin 3 π × 2 − 1 = 2 3 − 1
Area of each red acute triangle = 2 ( cot 3 π + cot 4 π ) ( 2 3 − 1 ) 2 = 8 9 − 8 5 3
Overlapping area = 4 3 3 − ( 8 9 − 8 5 3 ) × 2 = 2 3 − 4 9
Answer = 2 × 3 + ( − 9 ) × 4 = − 3 0