Scalene triangles and angle bisectors

Geometry Level 3

In a triangle $ABC$ , $AD$ is the internal angle bisector of $\angle A$ .

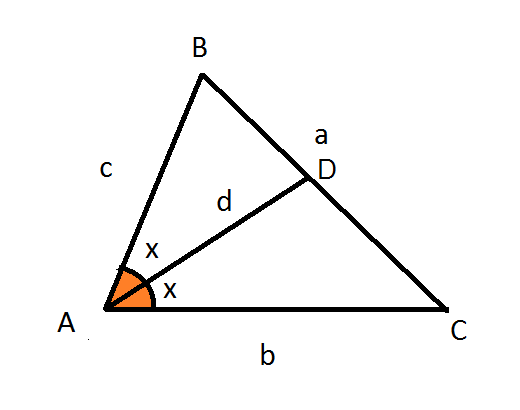
The sides $a$ , $b$ and $c$ are 6, 5 and 4 units respectively. If $d = \dfrac mn$ , where $m$ and $n$ are coprime positive integers. Then find $m + n$ .

The answer is 13.

2 solutions

Ajit Athle
Sep 2, 2017

d² = bc[1-a²/(b+c)²]= 4x5(1-6²/9²) ► d =10/3 units.

What is that formula called? never seen it before. Would be quite interested to see the derivation

Curtis Clement - 3 years, 9 months ago

Angle Bisector Length that is obtained by using Stewart's Theorem --- https://en.wikipedia.org/wiki/Stewart%27s_theorem. Let BD=m & DC=n. Then by the Angle Bisector Theorem: m=ac/(b+c) and n=ab/(b+c). Now we apply Stewart's Theorem to get: mb²+nc²=a(mn+AD²) which yields: a(AD²) = mb²+nc²- amn or AD²=(m/a)b²+(n/a)c²-mn=cb²/b+c)+bc² -a³bc/(b+c)²=bc[b/(b+c)+c/(b+c)-a²/(b+c)²]=bc[b(b+c)+c(b+c)-a²]/(b+c)²=bc[b²+2bc+c² -a²]/(b+c)²= bc[1-a²/(b+c)²]

Ajit Athle - 3 years, 9 months ago

Chew-Seong Cheong
Sep 3, 2017

By cosine rule , we have:

$\begin{aligned} a^2 & = b^2 + c^2 - 2bc\cos \angle A \\ 6^2 & = 5^2+4^2 - 2(5)(4) \cos 2x \\ \implies \cos 2x & = \frac {16+25-36}{40} = \frac 18 \\ \sin 2x & = \sqrt{1-\cos^2 2x}= \sqrt{1-\frac 1{8^2}} = \frac {3\sqrt 7}8 \\ \cos 2x & = 2\cos^2 x - 1 = \frac 18 \\ \implies \cos x & = \sqrt{\frac 9{16}} = \frac 34 \\ \sin x & = \sqrt{1-\cos^2 x} = \sqrt{1-\left(\frac 34\right)^2} = \frac {\sqrt 7}4 \end{aligned}$

The area of $\triangle ABC$ are given by:

$\begin{aligned} [ABC] & = \frac 12 bc \sin \angle A = \frac 12 (5)(4) \sin 2x = \frac {15\sqrt 7}4 \end{aligned}$

The area is also given by:

$\begin{aligned} [ABC] & = \frac 12 bd \sin x + \frac 12 cd \sin x \\ \implies \frac {15\sqrt 7}4 & = \frac {9\sqrt 7}8d \\ \implies d & = \frac {10}3 \end{aligned}$

$\implies m+n = 10 + 3 = \boxed{13}$

Scalene triangles and angle bisectors

The answer is 13.

2 solutions

0 pending reports