Scherzo

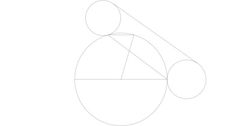The diagram shows two small circles tangent to a big circle at the ends of the longer chord as shown. The diameter of the big circle is 50. The diameter of the small circles are 19 and 21.

The shorter chord is parallel to the diameter of the big circle as shown, and its shortest distance from the diameter is 24.

The line segment which is not a chord ends at the center of the circle and one end of the shorter chord.

A tangent of the two small circles is drawn ending at the points of tangency as shown.

Find the length of the tangent, which can be expressed as $\frac{a\sqrt{b}}{c}$ in lowest terms, where $a$ , $b$ and $c$ are integers. Submit your answer as $a+b+c$ .