Schläfli symbols

Probability Level 2

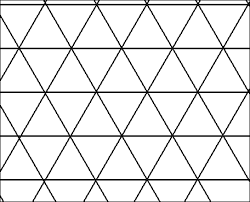
What is the dual of an infinite triangular lattice?

Definitions :

The dual of a solid with Schläfli symbols $\{m,n\}$ has Schläfli symbols $\{n,m\}.$
The Schläfli symbols for a geometric construct is defined by $\{m,n\}$ , where $m$ is the number of edges for each face and $n$ is the number of faces that meet at a vertex.

A single point A perfect sphere A rhomboidal lattice An infinite square lattice An infinite hexagonal lattice Itself It has no dual None of the above

1 solution

Geoff Pilling
Dec 21, 2016

The infinite triangular lattice has Schläfli symbols { $3,6$ }.

So the dual must have Schläfli symbols { $6,3$ }

This implies that each face has six sides, and three faces meet at every vertex, which describes $\boxed{\text{An infinite hexagonal lattice}}$