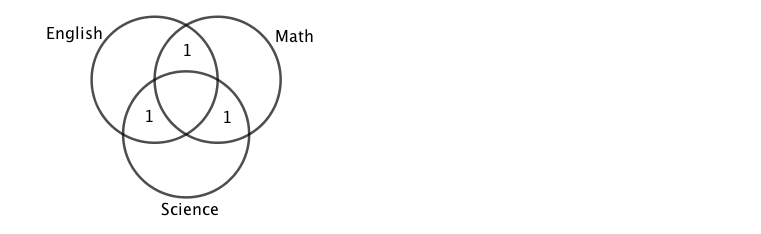School Time!

Logic Level 1

In a particular school, English, math, and science are taught to all students, where

  • some students who like English also like math;
  • some students who like math also like science;
  • some students who like science also like English.

Is there at least 1 student in the school who likes English, math, and science?

Yes, always No, not necessarily

Winston Choo by Winston Choo , 46, Singapore

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

8 solutions

Abraham Zhang
Nov 4, 2018

Here's a counterexample with 3 3 students in the school:

110 Helpful 3 Interesting 2 Brilliant 3 Confused

There could be student in the center, so it is possible to have a student that likes all three

Matt Titchenal - 2 years, 7 months ago

Log in to reply

The two options are "yes, always" and "no, not necessarily". This is justifying "not necessarily", which is different from "never".

Jason Dyer Staff - 2 years, 7 months ago

Log in to reply

You are correct

avik das - 2 years, 7 months ago

he who likes science likes English, who then likes maths

Brody Watkins - 2 years, 7 months ago

If a student likes maths, then he also likes English which means he will also like the left subject.

Rachit Bartwal - 2 years, 7 months ago

I didn't understand the solution 😑

Jishnu Ps - 2 years, 7 months ago

thank you. I can understand what 'some' means.

nay Song - 2 years, 7 months ago

hi hi hi hi hi hi hi hi hi hi hi hi hi hi hi hi hi hi hi

Zaryam Mirza - 2 years, 7 months ago

Log in to reply

u so weird

Zak Rasool - 2 years, 7 months ago

HI IHI IHIH HIHJ HIH HIHH H

Zak Rasool - 2 years, 7 months ago

hihi hnhi hih hi hi hih hi hi hi hi hi hi hi hi hi hi hi hi hi hi hi hi hi hi hi hi hi hi hi my name is jeff

Zak Rasool - 2 years, 7 months ago

Your venn diagram demonstrates that all the prepositions can be met without anyone liking all three subjects - very elegant solution.

Thomas Sutcliffe - 2 years, 4 months ago

If anyone likes English,then he likes math.He likes math and so he likes science.So he likes all of them.

Fahim Muhtamim - 1 year, 7 months ago
Avik Das
Nov 4, 2018

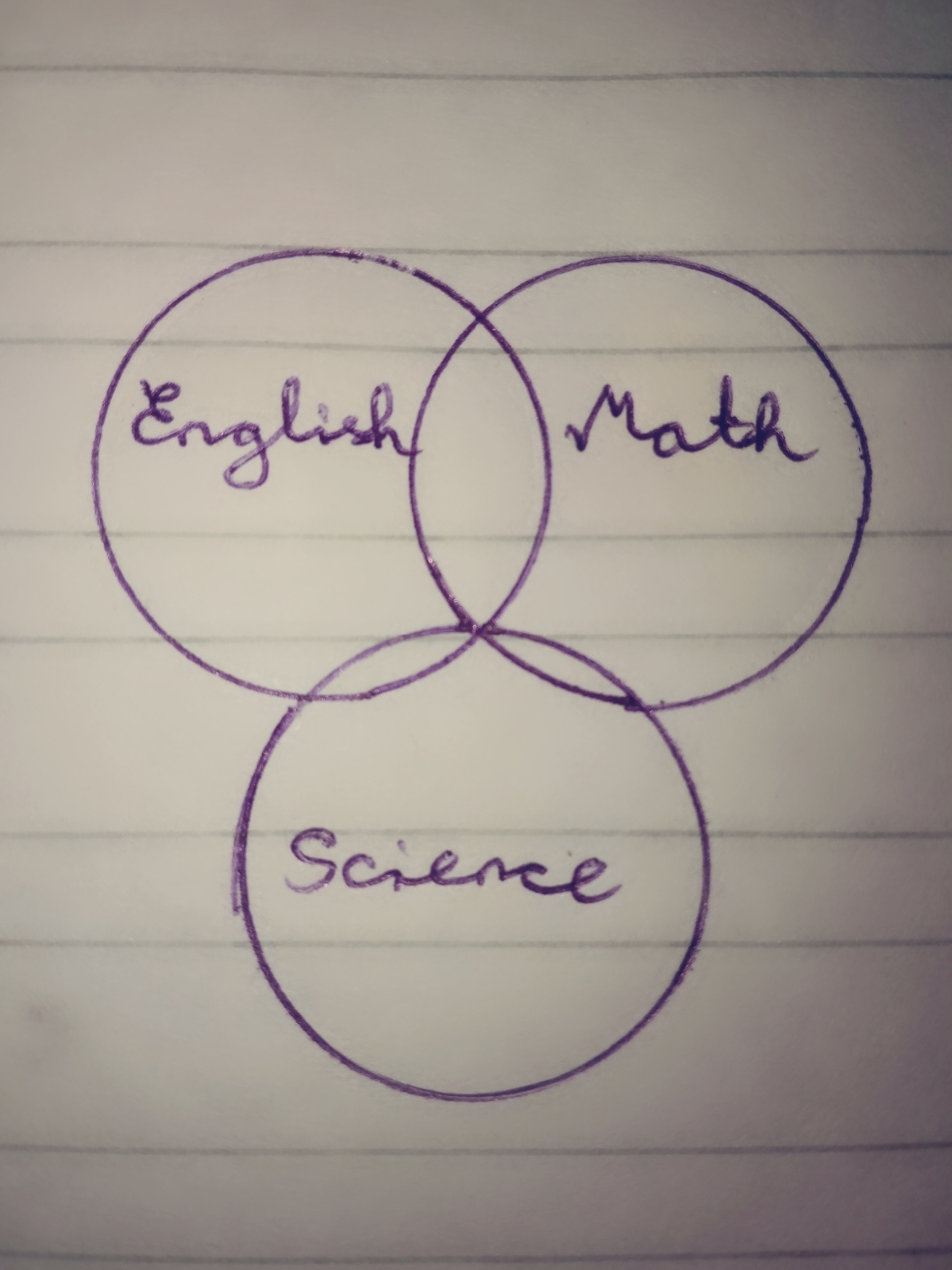In the above picture that situation rises in which no student likes English, mathematics and science at a time. hence​ the given statement should not be necessarily true.

48 Helpful 0 Interesting 1 Brilliant 0 Confused

This is the best of the Venn diagrams, because there is no universal intersection area. The others should simply write a 0 in this area.

Haim Michael Modiano - 2 years, 7 months ago

Bonus question: In the diagram, all circles have the same area and intersect at 1 point. Prove that the triangle formed by the second intersection between the circles has the same area with the triangle formed by the centers of the circles.

Hua Zhi Vee - 2 years, 7 months ago

Log in to reply

Connect the 3 centers and the 3 points of second intersection. This is a regular hexagon as all sides are equal radii and all interior angles are equal as figure has 3-fold symmetry.

Thus the diagonals are equal, and form 2 congruent equilateral triangles, which necessarily have equal areas.

QED

Steven Adler - 11 months, 2 weeks ago
Geoff Pilling
Oct 29, 2018

For example, you could have 2 students who like math and english only, 2 who like math and science only, and 2 who like science and english only.

15 Helpful 0 Interesting 0 Brilliant 0 Confused

If some students who like English also like Math, then they are a student who likes math and could also be students who like math and also like science. it never says anyone dislikes any subject as the answer implies.

Luke Marshall - 2 years, 7 months ago

Log in to reply

hmn.. thats what my dought is!

the real gamer - 2 years, 7 months ago
Zain Majumder
Nov 4, 2018

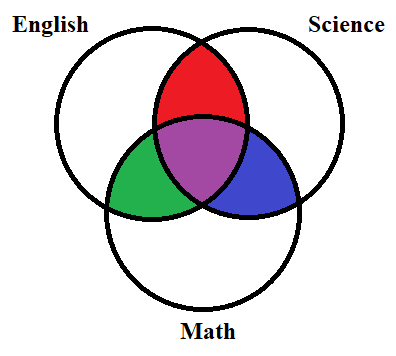
If a student likes two subjects, he must belong in the region contained by two circles. There are two regions of overlap between a pair of circles, one that is purple and one that is not. Therefore, to meet the requirements, it is not necessary that the students must be in the purple region (they can be in the red, green, or blue region instead).

3 Helpful 0 Interesting 0 Brilliant 0 Confused

With only partial knowledge of every student and no definite sample size, you can just put one in every given aspect and get a 0 on who likes all three subjects.

2 Helpful 0 Interesting 0 Brilliant 0 Confused
Melanie Topham
Nov 6, 2018

Because only “some” students who like English also like math, there is an implicit understanding that there are other students who like English but don’t like math.

It follows that there may be some students who only like English (or only like math, or only like science).

Therefore, this is definitely not a situation where there will “always” be a student who likes all 3 subjects (but there might be).

1 Helpful 0 Interesting 0 Brilliant 0 Confused
Emily Peng
Dec 28, 2019

The information is simply saying "some of A are B, some fraction of B is C, some fraction of C is A." But, a person may not always be part of that "some", so the answer is "No, not necessarily". Remember that "not necassarily" does not mean "never", it just means that it does not always have to be true.

0 Helpful 0 Interesting 0 Brilliant 0 Confused

The answer, "yes, always" is an absolute. There couldn't be an absolute.

0 Helpful 0 Interesting 0 Brilliant 0 Confused

Sometimes there is an absolute. For instance, if there are 3 students total, and 2 in the math class and 2 in the science class, there absolutely must be a student who takes both classes.

Steven Adler - 11 months, 2 weeks ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...