Tight Squares
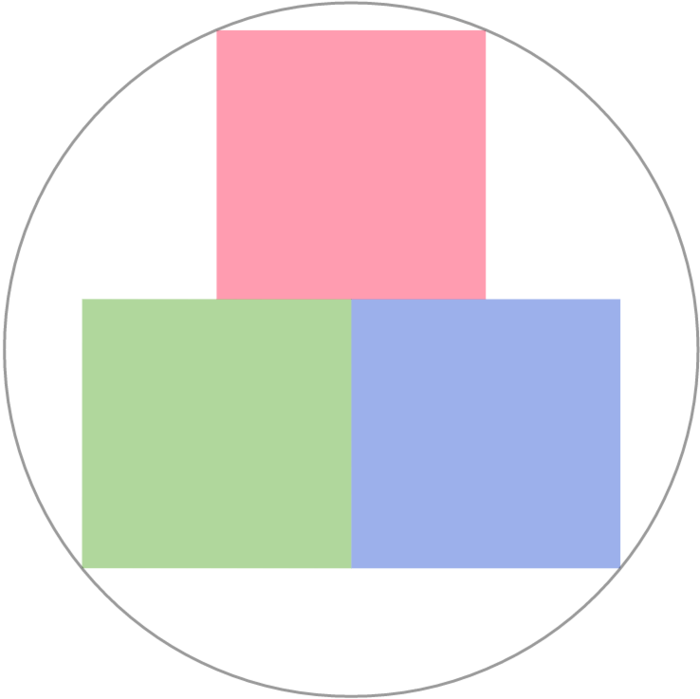
The figure shows a packing of three identical squares in a circle.
If we define Packing Efficiency = Total area of the container Total area of the packing material ,
To the nearest integer, how efficient (in percentage) is the packing in this case?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
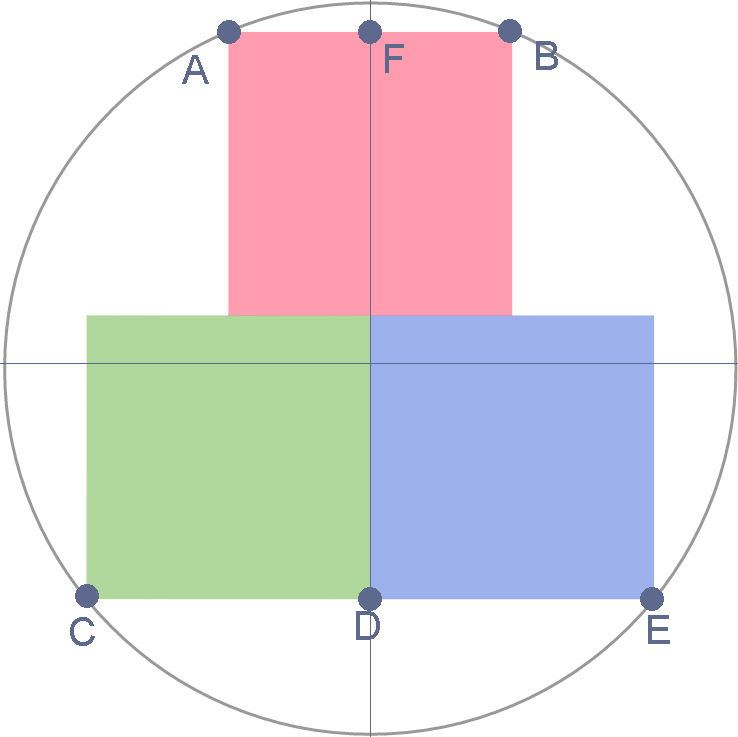 Without loss of generality, we could consider the unit circle described by
Without loss of generality, we could consider the unit circle described by
x 2 + y 2 = 1
So, points in the figure have coordinates
A ( − 2 t , 1 − 4 t 2 )
B ( 2 t , 1 − 4 t 2 )
C ( − t , − 1 − t 2 )
D ( 0 , − 1 − t 2 )
E ( t , − 1 − t 2 )
F ( 0 , 1 − 4 t 2 )
for − 1 ≤ t ≤ 1 , t ∈ R . Since the three squares are equals, we have that
C E = D F ⟹ 2 t = 1 − t 2 + 1 − 4 t 2 ⟹ t = 5 1 7 1 6
ignoring the negative solution. The value of t is exactly the side of the squares. Tha area of the circle is A c = π and the area of the squares is A s = 3 ( 5 1 7 1 6 ) 2 . Eventually Packing Efficiency = A c A s ⋅ 1 0 0 ≈ 5 7 %
For simplicity, we will use unit squares. First draw a vertical line splitting the circle in half. We can see that the diameter of the circle is equal to two plus a little extra on the top and a little extra on the bottom. We will label the extra bit at the top a, and the extra bit at the bottom b. Notice that by the geometric mean theorem, 1 = a ( 2 + b ) and 4 1 = b ( 2 + a ) . Solving this system and plugging into the formula P a c k i n g E f f i c i e n c y = π ( 1 + 2 a + 2 b ) 2 3 gives us the solution 57.52%.
Overlay a Cartesian coordinate system on the diagram where origin O is between the two bottom squares at the bottom, A is the top right corner of the top square, C is the bottom right corner of the right square, B M is the perpendicular bisector of A C at M , and B is the y -intercept of B M , as shown below.
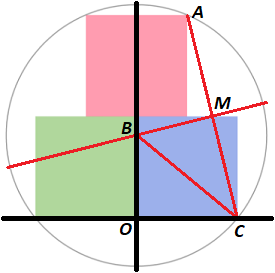
If s is the side length of one of the squares, then A has coordinates ( 2 1 s , 2 s ) and C has coordinates ( s , 0 ) . Chord A C has a slope of − 4 and its midpoint M has coordinates ( 4 3 s , s ) . The perpendicular bisector must then have an equation of y = 4 1 x + 1 6 1 3 s , which makes the coordinates of B ( 0 , 1 6 1 3 s ) , and O B = 1 6 1 3 s .
Since O B = 1 6 1 3 s and O C = s , then by Pythagorean's Theorem on △ O B C , B C = 1 6 5 7 s . Since B is the intersection of two perpendicular bisectors of chords, it is the center of the circle, and since C is a point on the edge of the circle, B C is a radius, and so the radius r of the circle is r = 1 6 5 7 s , and its area is 2 5 6 4 2 5 π s 2 .
Therefore, the packing efficiency is 2 5 6 4 2 5 π s 2 3 s 2 ≈ 5 8 % .
Simple.
Pythagorean theorem
can be used to solve this. By finding the length of the radius, the problem becomes trivial. Refer to the figure below.
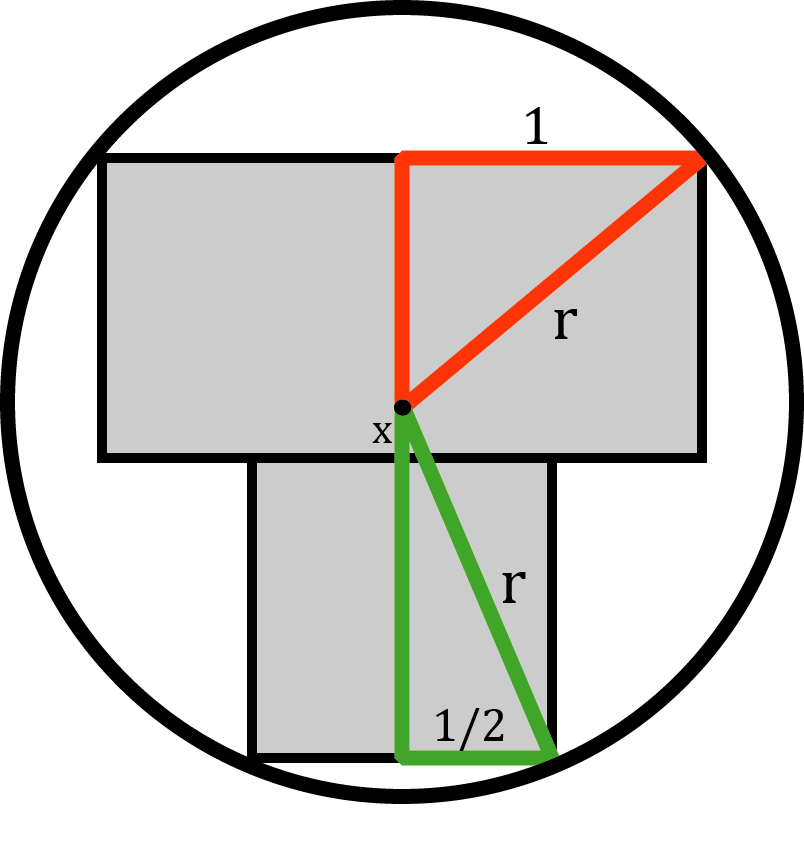
For simplicity, without losing generality, let the sides of the squares measure 1 unit . Let r be the radius of the circle, and x be the of distance from the center to the intersection point of the three squares.
Since the length of the sides of the squares is 1 unit, by Pythagorean theorem, we can see from the upper triangle that
upper triangle → r 2 = ( 1 − x ) 2 + 1 2 = x 2 − 2 x + 2 .
By the same logic, we can see that from the lower triangle, lower triangle → r 2 = ( 1 + x ) 2 + ( 1 / 2 ) 2 = x 2 + 2 x + 4 5 .
By equating the two equations, we can see that
RHS of upper triangle x 2 − 2 x + 2 4 x x = RHS of lower triangle = x 2 + 2 x + 4 5 = 4 3 = 1 6 3 units .
To get r , substitute x to the first equation, that is, of the upper triangle,
r 2 = ( 1 6 3 ) 2 − 2 ( 1 6 3 ) + 2 = 2 5 6 9 − 1 6 6 + 2 = 2 5 6 4 2 5 sq. units .
So, the area of the circle becomes A ∘ = 2 5 6 4 2 5 π sq. units .
To end, Parking Efficiency = A ∘ 3 A □ = 2 5 6 4 2 5 π sq. units 3 sq. units = 0 . 5 7 5 2 0 4 6 8 8 4 4 … ≈ 5 7 %
Note: Not to sound cocky, but I think this should be leveled down. Many people just don't attempt to solve a problem because of its level.
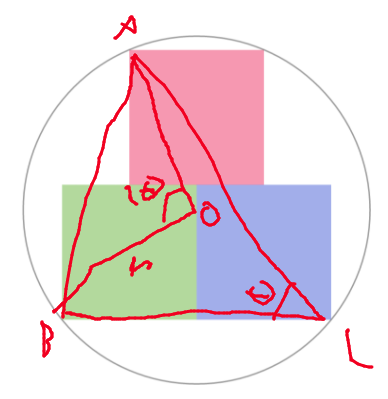 if we call one of the sides of the square
x
, then some lenghts are obvious. drop a perpendicular from
A
to
B
C
and then call the foot
D
. it is obvious that
B
D
=
2
x
,
D
C
=
2
3
x
,
A
D
=
2
x
→
A
B
=
(
2
x
)
2
+
(
2
x
)
2
=
x
2
1
7
,
A
C
=
(
2
x
)
2
+
(
2
3
x
)
2
=
2
5
x
now . for the right triangle
A
C
D
sin
(
θ
)
=
h
y
p
o
p
p
=
2
5
x
2
x
=
5
4
using laws of sine on
A
O
B
,
2
r
sin
(
θ
)
=
x
2
1
7
→
r
=
x
1
6
5
1
7
. the ratio of the area is
π
r
2
3
x
2
=
4
2
5
π
7
6
8
≈
5
7
%
if we call one of the sides of the square
x
, then some lenghts are obvious. drop a perpendicular from
A
to
B
C
and then call the foot
D
. it is obvious that
B
D
=
2
x
,
D
C
=
2
3
x
,
A
D
=
2
x
→
A
B
=
(
2
x
)
2
+
(
2
x
)
2
=
x
2
1
7
,
A
C
=
(
2
x
)
2
+
(
2
3
x
)
2
=
2
5
x
now . for the right triangle
A
C
D
sin
(
θ
)
=
h
y
p
o
p
p
=
2
5
x
2
x
=
5
4
using laws of sine on
A
O
B
,
2
r
sin
(
θ
)
=
x
2
1
7
→
r
=
x
1
6
5
1
7
. the ratio of the area is
π
r
2
3
x
2
=
4
2
5
π
7
6
8
≈
5
7
%
( 2 sin θ ) 2 + ( cos θ − 4 sin θ ) 2 4 sin 2 θ + cos 2 θ − 8 sin θ cos θ + 1 6 sin 2 θ 2 0 sin 2 θ + cos 2 θ − 8 sin θ cos θ 1 9 sin 2 θ + 1 − 8 sin θ cos θ 1 9 sin 2 θ 1 9 sin θ ⟹ tan θ = 1 2 = 1 = 1 = 1 = 8 sin θ cos θ = 8 cos θ = 1 9 8 Note that sin 2 θ + cos 2 θ = 1 For sin θ = 0
Therefore, sin θ = 4 2 5 8 , a = 4 2 5 1 6 , and the packing efficiency = π 3 a 2 = 4 2 5 π 3 × 1 6 2 ≈ 0 . 5 7 5 2 ≈ 5 8 %