SEAN and the TYrannosaurus Rex
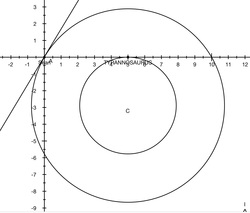 In this diagram, existing in the Cartesian plane, speedy SEAN is standing directly in the line of sight of a TYrannosaurus Rex. The dumb Tyrannosaurus is hungry, and it wants to eat Sean. Fortunately, Sean is a professional athlete who beat Usain Bolts' world record time by 5 seconds in last years Olympics. Also, the tyrannosaurus failed 1st grade and dropped out school that same year. The tyrannosaurus doesn't know how to do anything besides run directly at Sean (if Sean moves, the T-Rex will continue to run straight at his new position, thus its path will curve as Sean moves). Sean knows this, and decides to have a little fun. He wants to run in a perfect circle such that after one full rotation, he and the T-Rex end up in their respective starting places. At what angle (
A
in the picture) should Sean instantaneously start his circular run at.
In this diagram, existing in the Cartesian plane, speedy SEAN is standing directly in the line of sight of a TYrannosaurus Rex. The dumb Tyrannosaurus is hungry, and it wants to eat Sean. Fortunately, Sean is a professional athlete who beat Usain Bolts' world record time by 5 seconds in last years Olympics. Also, the tyrannosaurus failed 1st grade and dropped out school that same year. The tyrannosaurus doesn't know how to do anything besides run directly at Sean (if Sean moves, the T-Rex will continue to run straight at his new position, thus its path will curve as Sean moves). Sean knows this, and decides to have a little fun. He wants to run in a perfect circle such that after one full rotation, he and the T-Rex end up in their respective starting places. At what angle (
A
in the picture) should Sean instantaneously start his circular run at.
Assumptions:
Sean runs twice as fast as the Tyrannosaurus and the first instant he moves, he moves in the negative direction.
θ is in degrees and is of the interval ( − 9 0 , − 1 8 0 ) and is measured WRT the positive x-axis.
Sean is standing at (0,0) and the t-Rex is at ( x , 0 )
This is part of the set Trevor's Ten
The answer is -120.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
First physics problem, lol, not that good, but what the heck.
Because the T. rex will be constantly traveling at half Sean's speed, the radius of the circle it travels in will be half that of Sean's.
Also, since at all times the direction the Trex travels will be tangent to the circle he travels in, the radius from the center of the circle to the point of tangency (where it begins) will be perpendicular to the t-Rex's initial instantaneous direction. Thus the center of the trex's circle is located at (x,-y).
By observation, the circles they travel in will be concentric (this is very hard for me to explain. Anyone?).
Now, since ∠ S 0 T 0 C (note C denotes both the t-Rex's circle's center and Sean's circle's center) is 90 degrees, we have a right triangle, with hypotenuse S C and leg T 0 C . Since S C is twice T 0 C , we have a 30-60-90 triangle with the 30 being opposite T 0 C . Since tangents are perpendicular to their radius, we have θ = 9 0 + 3 0 = 1 2 0
The fact that they will travel in concentric circles is true; this is the case for a pursuit curve with k < 1 , where k is the ratio of the predator's to the prey's speeds.
Log in to reply
Ahh, thanks for clarifying that. Lol, as you can see, I'm new to this physics stuff.
The key to the solution is knowing that SEAN runs twice as fast as the T-Rex. If SEAN and the T-Rex both run around their circles and return back to their starting point at the same time, then the circumference of SEAN's path must be twice as big as the T-Rex's circle. Because C = 2 π r , the radius of each circle is proportional to it's circumference, meaning that the radius of SEAN's circle is twice that of the T-Rex's. Knowing this, we can add some lines to the picture to make things a little clearer. Let the length of the radius plotted from point C to (x,0) be R. This means that the length of the radius plotted from C to (0,0) is 2r. From here the answer is clear. We now have a right triangle in the 4th quadrant where one of the legs is R (the other being x) and the hypotenuse is 2R. The only kind of triangle that has a hypotenuse that is twice one of it's legs is a 30°-60°-90° triangle. The angle opposite of side R is 30°, which is -30° off of the x-axis, but we're trying to find the angle of the tangent line off of the x-axis. Well, our hypotenuse is a radius, and radii are perpendicular to tangent lines, meaning that our tangent line is another -90° off from the hypotenuse. Finally, add the two numbers together and you have your answer! ( − 3 0 ) ° + ( − 9 0 ) ° = ( − 1 2 0 ) °
I used the concept of relative velocity.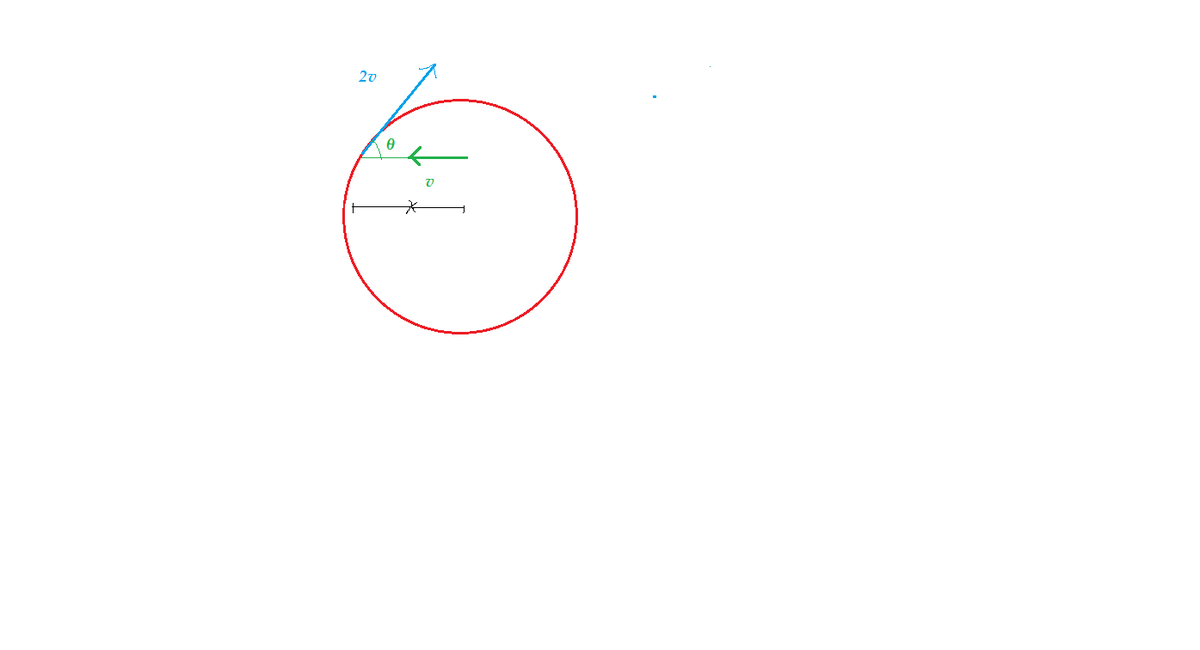
The separation between the Sean and Tyrannosaurus decreases at the rate of 2 v c o s θ + v
So − d t d x = ( 2 v c o s θ + v )
or ∫ 0 T ( 2 v c o s θ + v ) d t = − ∫ x x d x
Let T be the time when Sean has completed one revolution. Now as they return at their initial position so the distance between will remain unchanged. So the limits of integration of the term in RHS is from x to x .
So 2 v c o s θ = − v . Now as value of θ is between − 9 0 to − 1 8 0 .
So θ = − 1 2 0 .