Search for the Radius!

I will use the diagram below.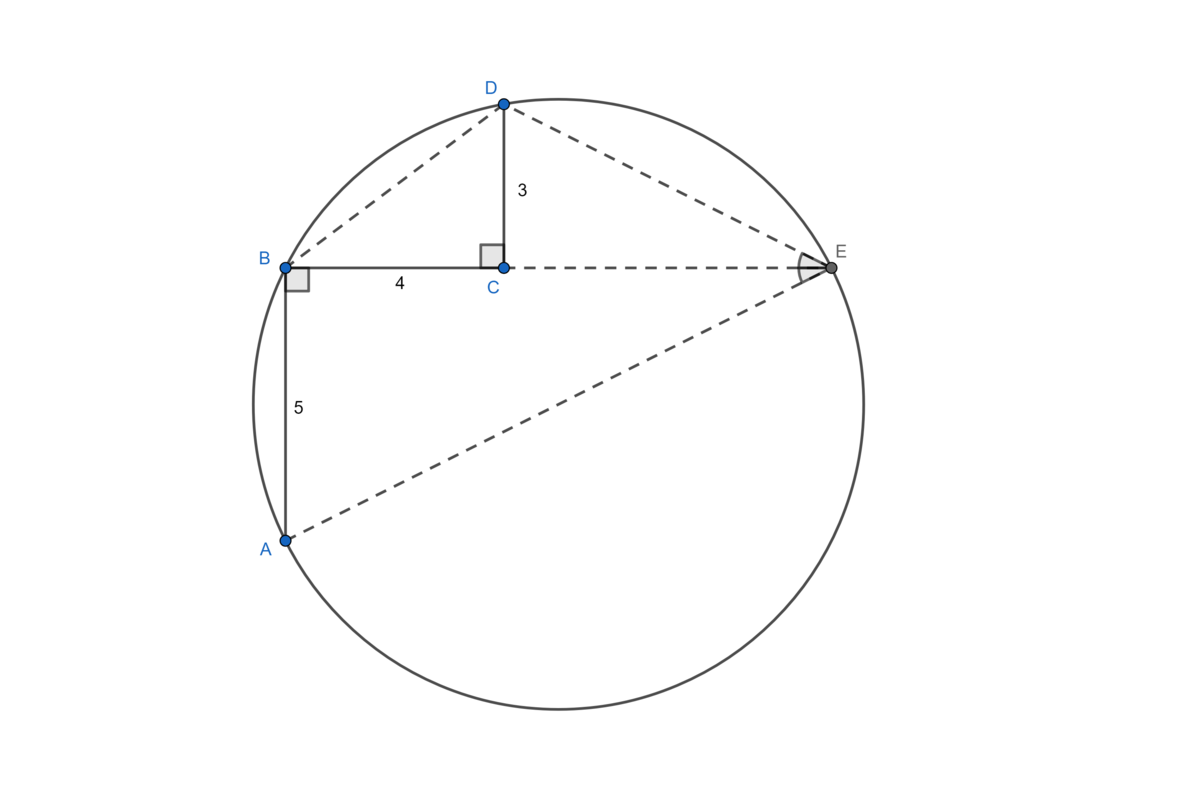 As shown in the diagram, extend $\overline{BC}$ and call it's intersection with the circle $E$ . Then, construct, $\overline{AE}$ , $\overline{DE}$ , and $\overline{BD}$ . By the Pythagorean Theorem, $BD = 5$ . Since $\angle BED$ and $\angle AEB$ intercept congruent chords, they also intercept congruent arcs and are therefore congruent angles.

Now, $\triangle ABE \sim \triangle DCE$ . Let $CE = x$ . Since the ratios of corresponding sides of similar triangles are equal, $\begin{aligned} \frac{AB}{DC} &= \frac{BE}{CE} \\ \frac{5}{3} &= \frac{4+x}{x} \\ 5x &= 12 + 3x \\ x &= 6 \end{aligned}$ Thus $BE = 10$ . Since $\angle ABE$ is a right angle, $AE$ is a diameter of the circle. By the Pythagorean Theorem, $\begin{aligned} AE &= \sqrt{AB^2 + BE^2} \\ &= \sqrt{5^2 + 10^2} \\ &= \sqrt{125} \\ &= 5^{^3\!/\!_2} \end{aligned}$ Therefore the radius of the circle is $\dfrac{5^{^3\!/\!_2}}{2}$ and we have $p=5$ , $q=3$ and $r=2$ . Finally, $p+q+r = 5 + 3 + 2 = \boxed{10}$ .