A classical mechanics problem by Bhaskar Kumawat

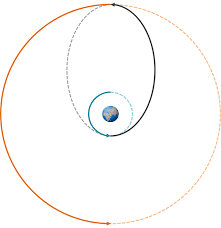
A Hohmann Transfer is an orbital manoeuvre performed by orbiting spacecrafts to extend (or contract) their orbits in the most fuel efficient way as possible.

It involves applying impulses (or velocity changes) two times. First, to extend the orbit to convert it into a highly eccentric ellipse (black line) that takes the craft to the second orbit and then the second one to circularize to achieve the target radius(red line).

To maintain maximum possible efficiency, the second impulse is given directly opposite to the first impulse (on the "backside" of the orbit).

The energy required for such transfer is proportional to the sum of the velocity changes required at both points.

Assuming the initial radius to be $R$ .

Find the ratio of the final radius to $R$ such that the energy required to accomplish such a transfer is maximum.

Assume that the initial and final orbits are always circular.

---

You can use a calculator if you like.