Seating arrangments
Probability
Level
2
Marvin, Peter , Juan, Jose and Ana are randomly seated in a row of five seats. What is the probability that Marvin and Juan are seated at the end seats?
The answer is 0.1.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
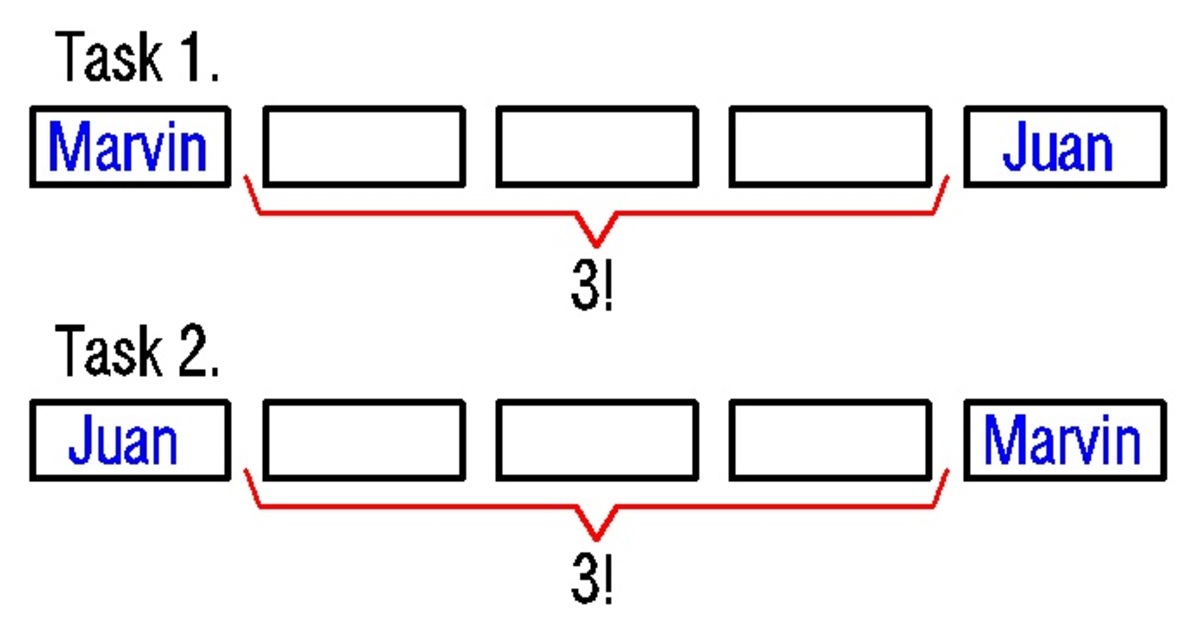
First consider the probability that either gets on one of the ends and then that, out of the remaining people, the other of the pair sits at the other end:
.4*.25=.1