Secants of a circle
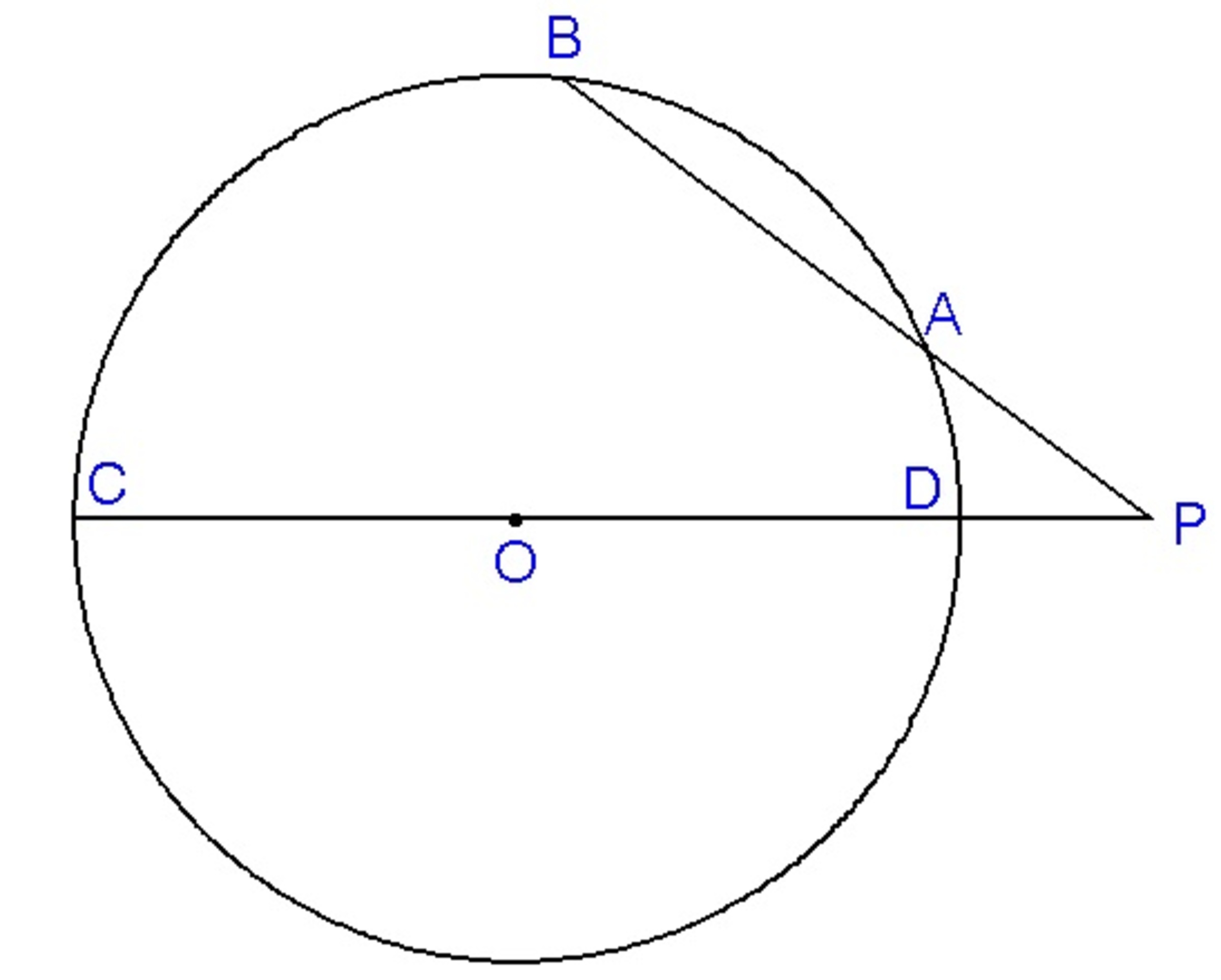 The diameter of the circle shown above is
C
D
. If
C
D
=
7
4
,
C
P
=
7
7
, and
P
B
=
3
3
, what is the measure of
∠
B
P
C
in degrees?
The diameter of the circle shown above is
C
D
. If
C
D
=
7
4
,
C
P
=
7
7
, and
P
B
=
3
3
, what is the measure of
∠
B
P
C
in degrees?
note: The figure is not drawn to scale.
The answer is 60.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
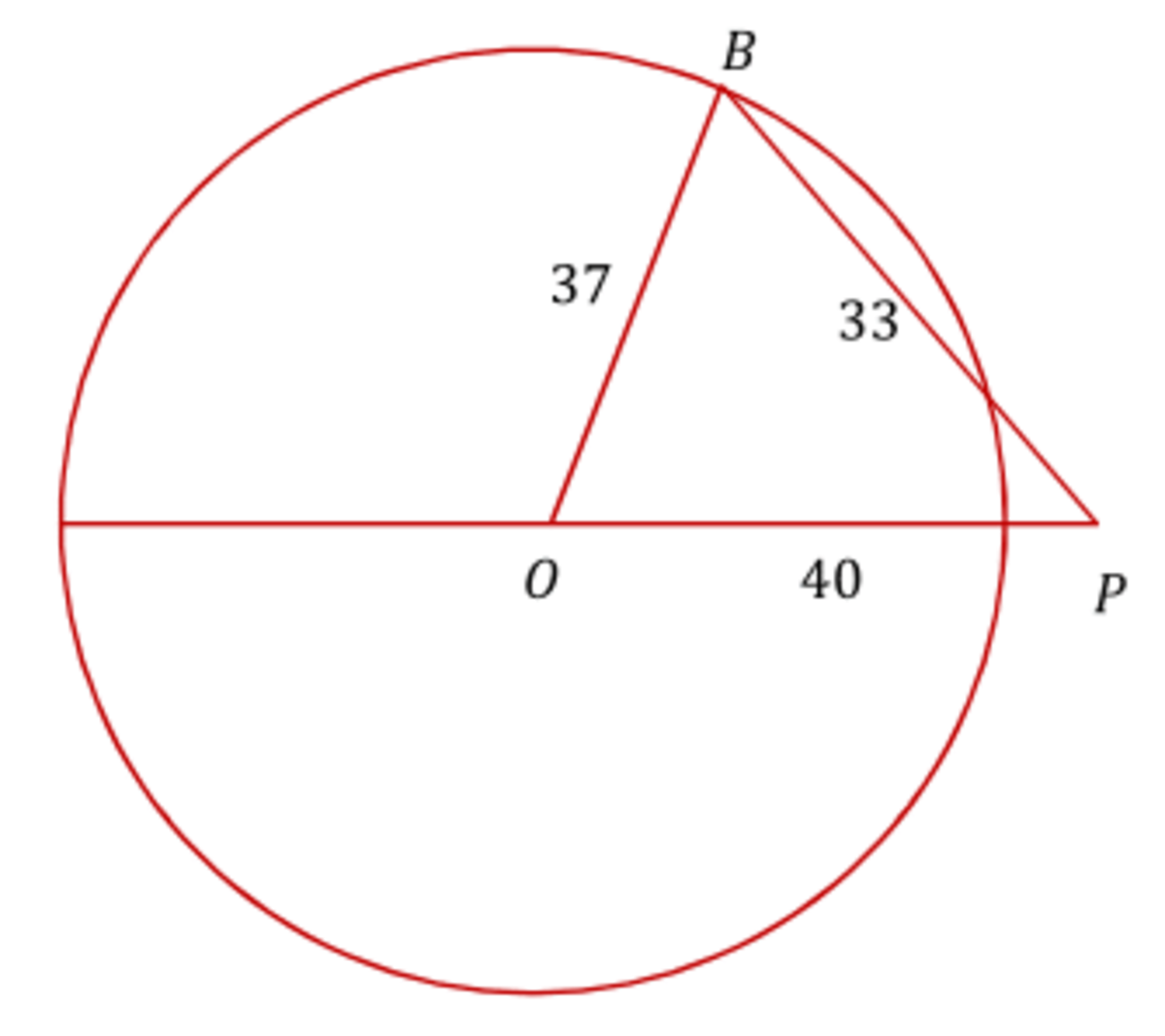 Triangle
O
P
B
has sides
Triangle
O
P
B
has sides
B P = 3 3
O B = 2 1 × 7 4 = 3 7
O P = 3 7 + 3 = 4 0
From a law of cosines
cos ( ∠ O P B ) = 2 × 4 0 × 3 3 4 0 2 + 3 3 2 − 3 7 2 = 2 1
∠ O P B = arccos 2 1 = 6 0 ∘
(
D
P
)
=
(
C
P
)
−
(
C
D
)
=
7
7
−
7
4
=
3
(
O
D
)
=
2
(
C
D
)
=
3
7
(
O
A
)
=
(
O
D
)
=
3
7
(
O
P
)
=
(
O
D
)
+
(
D
P
)
=
3
7
+
3
=
4
0
(
P
A
)
(
P
B
)
=
(
P
D
)
(
P
C
)
⇒
(
P
A
)
⋅
3
3
=
3
⋅
7
7
⇒
(
P
A
)
=
7
If
θ
is the angle we are looking for then by applying the cosine law on the triangle OAP we get:
(
O
A
)
2
=
(
O
P
)
2
+
(
P
A
)
2
−
2
⋅
(
O
P
)
(
P
A
)
cos
θ
⇒
1
3
6
9
=
1
6
0
0
+
9
−
2
⋅
4
0
⋅
7
⋅
cos
θ
⇒
cos
θ
=
2
1
⇒
θ
=
6
0
∘
( P A ) ( 3 3 ) = ( 3 ) ( 7 7 ) ⟹ P A = 7
Therefore, B A = 3 3 − 7 = 2 6 .
A line perpendicular to a chord of a circle and containing the center of the circle, bisects the chord and its major and minor arcs. Thus,
B E = A E = 1 3
In right △ P E O , P O = 4 0 and P E = 2 0 .
It follows that,
cos ∠ B P C = 4 0 2 0 ⟹ ∠ B P C = cos − 1 ( 2 1 ) = 6 0 ∘