Second Order Filter - Power Dissipation
This is a follow-up to the original problem by Hosam Hajjir. The filter circuit below takes a sinusoidal input voltage at angular frequency and produces a sinusoidal output voltage.
At , effectively no active power is dissipated in the circuit. At , the circuit dissipates the maximum possible active power . At what angular frequency does the circuit dissipate active power equal to ?
Note: Assume the same input voltage magnitude for all trials
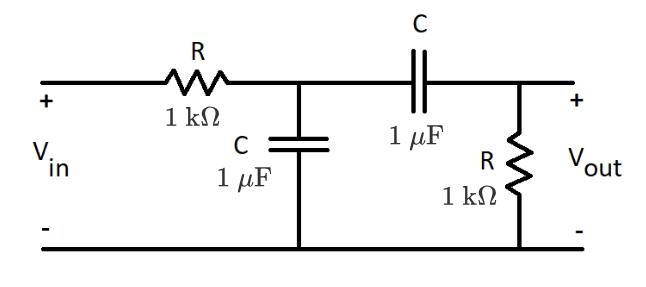
The answer is 550.25.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
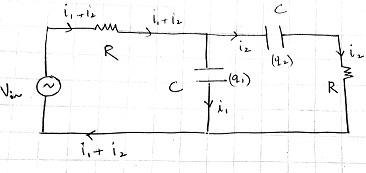


When the angular frequency is infinite, the equivalent circuit is just the input voltage dropped over one of the resistors. This is the maximum power condition.
Sweep over the angular frequency and store the value of the angular frequency which results in a total power dissipation equal to half of the maximum possible value. The answer turns out to be 5 5 0 . 2 5 rad/s .
Z C = − ω C j Z 1 = R + Z C Z 2 = Z 1 + Z C Z 1 Z C V 1 = V i n R + Z 2 Z 2 V o u t = V 1 R + Z C R V R 1 = V i n − V 1 P = R ∣ V R 1 ∣ 2 + R ∣ V o u t ∣ 2