Second Point Of Intersection Of Circumcircles
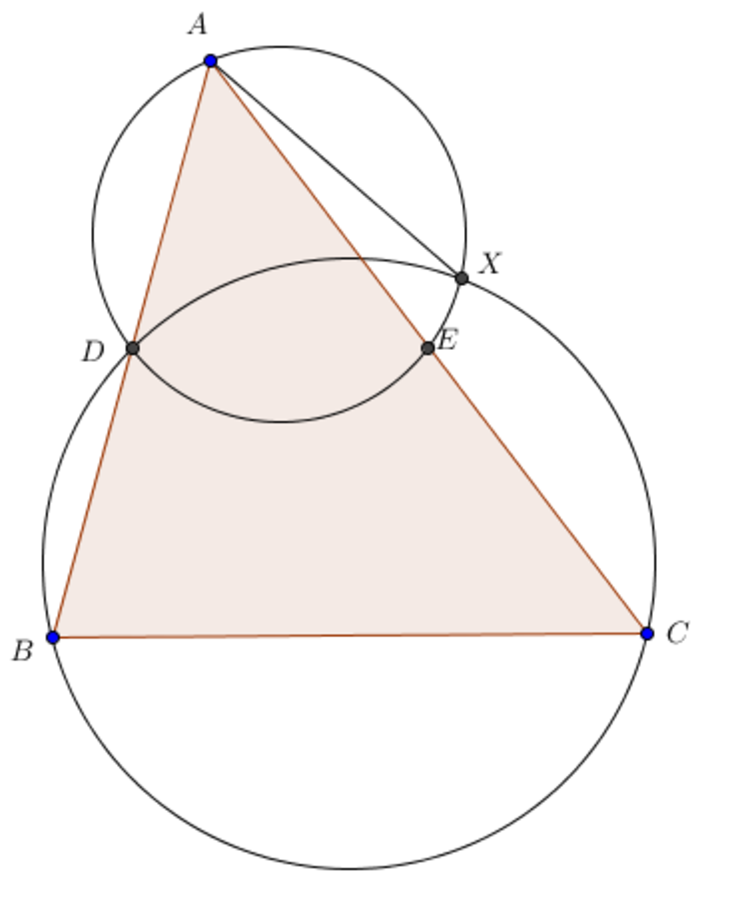 Let
△
A
B
C
be a triangle with
B
C
=
5
,
C
A
=
6
,
A
B
=
7
.
Let
D
,
E
be the midpoints of
A
B
,
A
C
respectively. The circumcircles of
△
B
C
D
and
△
A
D
E
meet for a second time at
X
(
X
=
A
). Given that
A
X
2
=
b
a
for some coprime positive integers
a
,
b
,
find the last three digits of
a
+
b
.
Let
△
A
B
C
be a triangle with
B
C
=
5
,
C
A
=
6
,
A
B
=
7
.
Let
D
,
E
be the midpoints of
A
B
,
A
C
respectively. The circumcircles of
△
B
C
D
and
△
A
D
E
meet for a second time at
X
(
X
=
A
). Given that
A
X
2
=
b
a
for some coprime positive integers
a
,
b
,
find the last three digits of
a
+
b
.
Details and assumptions
- This problem is inspired by a recent problem that appeared in the Chinese Girls Mathematical Olympiad 2014.
The answer is 883.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Yes u are right
Very nice solution. I'm adding one in Cartesian coordinates. Embed △ A B C into the first quadrant of a Cartesian coordinate system with origin in B and the directed line B C as x -axis. Apply cosine rule to triangle △ A B C to get 2 5 + 4 9 − 2 ⋅ 5 ⋅ 7 ⋅ cos ∠ A B C = 3 6 , hence cos ∠ A B C = 3 5 1 9 and consequently sin 2 ∠ A B C = 1 − 3 5 2 1 9 2 = 1 2 2 5 8 6 4 . Use Apollonius' theorem to the median C D , obtaining C D 2 = 4 2 ⋅ 5 2 + 2 ⋅ 6 2 − 7 2 = 4 7 3 If R is the circumradius of △ B C D , by sine rule we have 4 R 2 = sin 2 ∠ A B C C D 2 \hbox , w h e n c e R 2 = 1 3 8 2 4 1 2 5 1 9 5 Call F the circumcenter of △ B C D and J its x -projection. Then F J 2 = R 2 − 4 2 5 = 1 3 8 2 4 3 0 2 5 , hence the coordinates of F are ( 5 / 2 , 5 5 6 / 2 8 8 ) . Call I the x -projection of A , to get ∣ B I ∣ = ∣ A B ∣ cos ∠ A B C = 7 ⋅ 3 5 1 9 = 5 1 9 . Now if L is the x -projection of E , then ∣ B L ∣ = 2 1 ⋅ ( 5 + 2 1 9 ) = 5 2 2 . Now, if G is the circumcenter of △ A D E and N its x -projection, abscissa of G is given by ∣ B N ∣ = 2 ∣ B K ∣ + ∣ B L ∣ = 2 0 1 9 + 4 4 = 2 0 6 3 , where K is the x -projection of D . Let's call now r the circumradius of △ A D E . We get 4 r 2 = sin 2 ∠ A D E 3 2 = sin 2 ∠ A B C 3 2 \hbox , h e n c e r 2 = 3 8 4 1 2 2 5 If O is the mid-point of D E , we get G O 2 = r 2 − 4 D E 2 = 3 8 4 1 2 2 5 − 1 6 2 5 = 3 8 4 6 2 5 , hence ∣ G O ∣ = 4 8 2 5 6 . Moreover, we have D K 2 = ( 2 7 ) 2 sin 2 ∠ A B C = 2 5 2 1 6 , hence D K = 5 6 6 . The coordinates of point G are given by G : ( 2 0 6 3 , 5 6 6 + 4 8 2 5 6 ) = ( 2 0 6 3 , 2 4 0 4 1 3 6 ) . The system of equations of the two circumcircles is ⎩ ⎪ ⎨ ⎪ ⎧ ( x − 2 5 ) 2 + ( y − 2 8 8 5 5 6 ) 2 = 1 3 8 2 4 8 9 4 2 5 ( x − 2 0 6 3 ) 2 + ( y − 2 4 0 4 1 3 6 ) 2 = 3 8 4 1 2 2 5 The solution different from D is the point X : ( 4 0 8 1 1 5 9 0 5 , 4 0 8 1 4 0 2 0 6 ) and its squared distance to A is given by d 2 = ( 4 0 8 1 1 5 9 0 5 − 5 1 9 ) 2 + ( 4 0 8 1 4 3 2 0 6 − 5 1 2 6 ) 2 = = 5 8 3 6 3 0 0 = b a . Now the last three digits of a + b = 6 8 8 3 are 8 8 3 .
I hope. This answer is wrong. Make second approach triangle BEC similar to triangle ADX so AX.AX=931/100 so answer will be 031
Log in to reply
I find no particular reason why △ B E C should be similar to △ A D X . They have only one common angle ( ∠ A C D = ∠ A E D = ∠ E C B ). The following image disproves your claim.
 Image link: http://s23.postimg.org/4axu1538b/Untitled.png
Image link: http://s23.postimg.org/4axu1538b/Untitled.png
OK, this is a horrible problem with a very inelegant solution. Apologies. The original problem asked to show that the second intersection point of the circumcircles of △ B C D , △ A D E and △ B C E , △ A D E are equidistant from A (which should be obvious from the following solution). The reader might refer to this helpful article on barycentric coordinates.
Set the normalized barycentric coordinates A = ( 1 , 0 , 0 ) , B = ( 0 , 1 , 0 ) , C = ( 0 , 0 , 1 ) . Then, the coordinates of D , E are ( 2 1 , 2 1 , 0 ) and ( 2 1 , 0 , 2 1 ) respectively.
Suppose the equation of circle ( A D E ) is a 2 y z + b 2 z x + c 2 x y = u x + v y + w z (normalized coordinates). Plugging the coordinates of A , we see that u = 0 . Plugging the coordinates of D , we see that 4 c 2 = 2 u + v ⟹ v = 2 c 2 . Similarly, plugging the coordinates of E shows that w = 2 b 2 . To sum it up, the equation of the circumcircle of △ A D E is a 2 y z + b 2 z x + c 2 x y = 2 c 2 y + b 2 z .
Let the equation of ( B C D ) be a 2 y z + b 2 z x + c 2 x y = p x + q y + r z . Plugging the coordinates for B and C show that q = r = 0 . Plugging the coordinates of D , we see that 4 c 2 = 2 p ⟹ p = 2 c 2 . To sum it up, the equation of the circumcircle of △ B C D is a 2 y z + b 2 z x + c 2 x y = 2 c 2 x .
Let ( x , y , z ) be the point of intersection of ( A D E ) and ( B C D ) apart from D (where x + y + z = 1 ).
The displacement vector A X is ( x − 1 , y , z ) , so ∣ A X ∣ 2 = − a 2 y z − b 2 z ( x − 1 ) − c 2 ( x − 1 ) y = − ( a 2 y z + b 2 z x + c 2 x y ) + ( b 2 z + c 2 y ) = − 2 c 2 y + b 2 z + b 2 z + c 2 y = 2 b 2 z + c 2 y = a 2 y z + b 2 z x + c 2 x y = 2 c 2 x .
Now, we know that x , y , z simultaneously satisfy the equations a 2 y z + b 2 z x + c 2 x y a 2 y z + b 2 z x + c 2 x y x + y + z = 2 c 2 x = 2 c 2 y + b 2 z = 1 . Equating a 2 y z + b 2 z x + c 2 x y from the first two equations and plugging z = 1 − x − y , we obtain c 2 x = c 2 y + b 2 ( 1 − x − y ) ⟹ y = c 2 − b 2 ( b 2 + c 2 ) x − b 2 .
This implies z = 1 − c 2 − b 2 ( b 2 + c 2 ) x − b 2 − x = b 2 − c 2 c 2 ( 2 x − 1 ) .
Plugging this in the second equation, we obtain 2 a 2 c 2 − b 2 ( b 2 + c 2 ) x − b 2 b 2 − c 2 c 2 ( 2 x − 1 ) + 2 b 2 c 2 − b 2 ( b 2 + c 2 ) x − b 2 x + 2 c 2 c 2 − b 2 ( b 2 + c 2 ) x − c 2 x = 0 .
We interpret this as a quadratic in x . We know that x = 2 1 is one solution (since D = ( 2 1 , 2 1 , 0 ) is a point of intersction of the circles in question). To find the other solution, it suffices to find the ratio of the constant term and coefficient of x 2 . Collecting terms, we find out that this ratio is [ x 2 ] [ x 0 ] = 2 a 2 ( b 2 + c 2 ) − ( b 2 − c 2 ) 2 a 2 b 2 . Hence, the other solution for x is 2 a 2 ( b 2 + c 2 ) − ( b 2 − c 2 ) 2 2 a 2 b 2 . Now, ∣ A X ∣ 2 = 2 c 2 x = 2 a 2 ( b 2 + c 2 ) − ( b 2 − c 2 ) 2 a 2 b 2 c 2 .
Plugging the values shows us that the last three digits of a + b are 8 8 3 .
Note that the expression of A X 2 is symmetric in b , c , which solves the original problem.