Second problem

We have inequality of form x^y + y^x >= 1 for positive reals x and y so use inequality to get answer

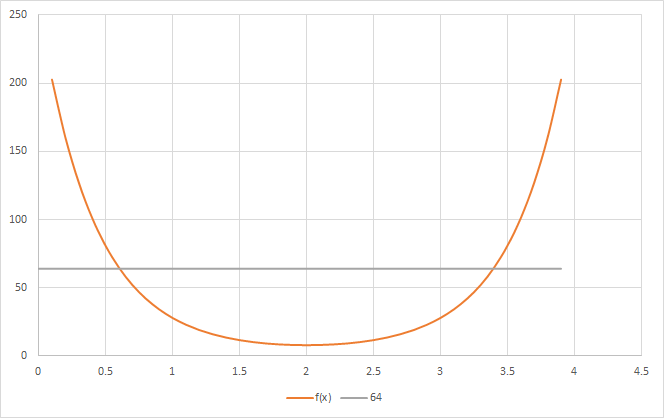
Let $f(x) = x^x + y^y$ , where $x+y=4$ . Then $f(x) = x^x + (4-x)^{4-x}$ and $f'(x) = (\ln x +1)x^x - (\ln(4-x)+1)(4-x)^{4-x}$ . We note that $f'(x) > 0$ or $f(x)$ is increasing for $x \in (3,4)$ . Now, note that $f(3) = 3^3 + 1^1 = 28$ and $f(3.4) = 3.4^{3.4} + 0.6^{0.6} \approx 64.861$ . Implying that $f(x) = 64$ for $3 < x < 3.4$ . In fact $f(x)=64$ when $x \approx 3.393901832$ and $y \approx 0.606098169$ . Since $x$ and $y$ are identical in the system of equations. $x \approx 0.606098169$ and $y \approx 3.393901832$ is a also a solution pair.

Answer: Yes there are real value pairs $(x,y)$ satisfying the system of equations.