Arc Trail
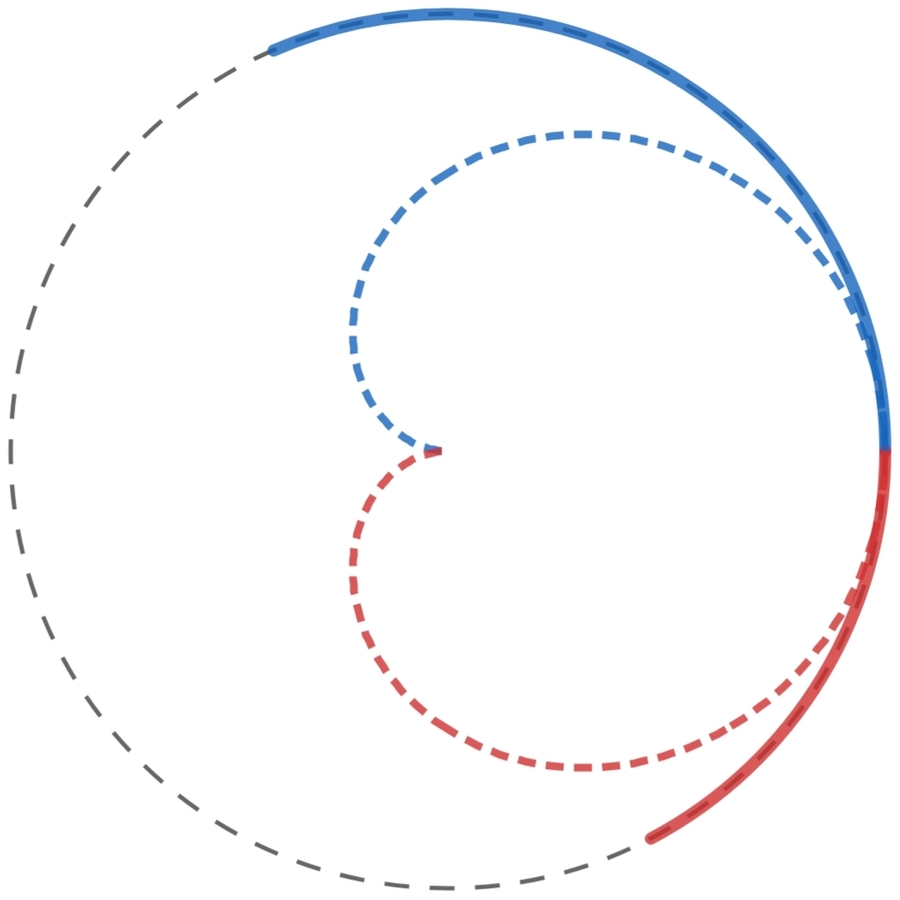
Circular arcs are drawn from a fixed point on the circumference of a unit circle.
What is the area bounded by the locus (shown in dotted blue and red) of the center of masses of the circular arcs?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Shouldn't it be d x instead of d θ in the last few integrals?
Log in to reply
Yes, that was a typo. Thanks for letting me know.
Let the arc subtend an angle of ϕ and arc length ϕ . Therefore the end points of the arc are ( 0 , 0 ) and ( cos ϕ , sin ϕ ) .
For points ( cos t , sin t ) along the arc, the average x-coordinate is given by ϕ 1 ∫ 0 ϕ cos t d t = ϕ sin ϕ while the average y-coordinate is given by ϕ 1 ∫ 0 ϕ sin t d t = ϕ 1 − cos ϕ Therefore the centre of mass is the point ( ϕ sin ϕ , ϕ 1 − cos ϕ ) . We will find the locus in polar coordinates: x = ϕ sin ϕ y = ϕ 1 − cos ϕ θ = tan − 1 ( x y ) = tan − 1 ( sin ϕ 1 − cos ϕ ) = tan − 1 ( tan 2 ϕ ) = 2 ϕ r ∴ r = x 2 + y 2 = ϕ 2 sin 2 ϕ + cos 2 ϕ − 2 cos ϕ + 1 = ϕ 2 − 2 cos ϕ = ϕ 2 − 2 + 4 sin 2 2 ϕ = ϕ 2 sin 2 ϕ = θ sin θ Now to find the area of this curve, we use the formula for area in polar coordinates: A = ∫ α β 2 1 r 2 d θ 2 ∫ 0 π 2 1 θ 2 sin 2 θ d θ ∫ 0 π θ 2 2 1 ( 1 − cos 2 θ ) d θ ∫ 0 2 π x 2 1 − cos x d x [ − x 1 − cos x ] 0 2 π − ∫ 0 2 π − x sin x d x = 0 + x → 0 lim x 1 − cos x + ∫ 0 2 π x sin x d x = 0 + x → 0 lim 1 sin x + ∫ 0 2 π x sin x d x = ∫ 0 2 π x sin x d x ( by letting x = 2 θ ) ( using integration by parts ) ( using L’Hospital’s rule )