Sectors, Bisectors, and a Touch of Trigonometry
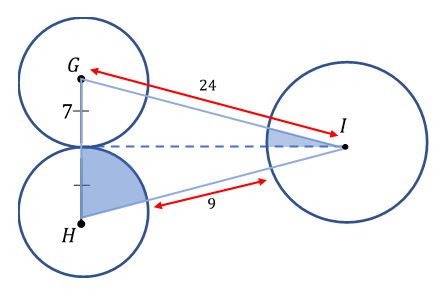
In the figure (not drawn to scale) above, circles and are tangent and congruent to each other with a radius of 7 units. Triangle is isosceles with two of its sides measuring 24 units, and the distance from the endpoints of circles and span 9 units. A bisector line is drawn from the point of tangency to center point .
Find the total area of the shaded regions (round off to 1 decimal place).
Bonus: Find the length of the bisector line.
The answer is 40.7.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Focus on triangle G I H first. The main objective to solving this problem is finding the sum of the areas of the sectors of the involved circles. Since an angle is required to find the areas of the sectors, use trigonometry to find the angles first.
Since the dashed line bisects the line G H , it is perpendicular--thus, we have a right triangle with the hypotenuse equal to 2 4 (since it is isosceles, two sides must be equal) and one of its legs equal to 7 (the radius of the circle). Since we are only solving for half the angle we need, let angle ∠ I = 2 θ
We can solve for theta by using the common trigonometric identities,
sin ( 2 θ ) = 2 4 7
2 θ = sin − 1 ( 2 4 7 )
2 θ = 1 6 . 9 5 7 ∘
θ I ≈ 3 3 . 9 1 5 ∘
Next, we find the angle associated with circle H's sector. Focus again on the whole triangle G I H .With the law of sines, we have the following equation:
sin 3 3 . 9 1 5 1 4 = sin θ 2 4
sin θ = 1 4 2 4 sin 3 3 . 9 1 5
θ = sin − 1 ( 1 4 2 4 sin 3 3 . 9 1 5 )
θ H ≈ 7 3 . 0 4 ∘
We now have solved for the angles we need, so we can now use the formula for the area of a sector of circle:
A = π r 2 ( 3 6 0 θ )
Area of Sector H,
A H = π ⋅ 7 2 ( 3 6 0 7 3 . 0 4 )
A H ≈ 3 1 . 2 3 sq. units
Area of Sector I,
But first we must find its radius:
If H I = G I = 2 4 , then
r h + d + r i = H I = 2 4
where:
r h = radius of circle H = 7
d = distance from the two endpoints of circles H and I = 9
r i = radius of circle I
Therefore:
7 + 9 + r i = 2 4
r i = 8 units
Now that we have solved for its radius, we can proceed to the area:
A I = π ⋅ 8 2 ( 3 6 0 3 3 . 9 1 5 )
A I ≈ 1 8 . 9 4 1 sq. units
Since we're only looking for half the area (bisected by the line),
2 A I = 2 1 8 . 9 4 1
2 A I = 9 . 4 7 sq. units
Finally,
A s h a d e d = A H + 2 A I
A s h a d e d = 3 1 . 2 3 + 9 . 4 7
A s h a d e d ≈ 4 0 . 7 sq. units
For the bonus question:
Go back to the right triangle earlier. The bisector line is one of the legs of a right triangle with hypotenuse 2 4 and another leg 7 . By the Pythagorean Theorem,
let x = the length of the bisector line
2 4 2 = x 2 + 7 2
x 2 = 2 4 2 − 7 2
x = 2 4 2 − 7 2
x = 5 2 7 or ≈ 2 2 . 9 5 6 units