Sectors in Triangle
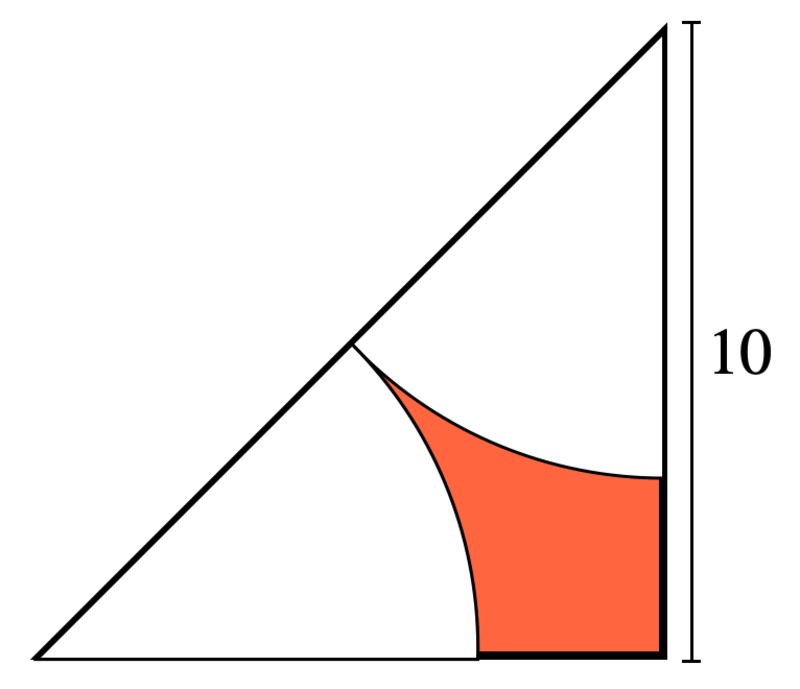
Two sectors of a circle are inscribed in an isosceles right triangle with length of the legs of 1 0 . What is the area of the red region to the nearest integer ?
The answer is 11.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
Nice one sir
hypotenuse = diameter = 1 0 2 [ by pythagorean theorem ]
radius of circular sector = 2 1 0 2 = 5 2
area of red part = area of right triangle - area of two circular sectors
area of red part = [ 2 1 × base × height ] − [ 3 6 0 θ × π × r 2 ]
area of red part = [ 2 1 × 1 0 × 1 0 ] − [ 3 6 0 9 0 × π ( 5 2 ) 2 ] ≈ 1 1 square units
Main: colored region = Area of Triangle - 2 (sector)
AoT: given by b*h/2
sector: requires radius, from below we have radius, area of sector given by (area of circle with given radius)/8. We divide by 8 because isosceles, and right angle implies other two angles pi/4 which is 1/8 of 2pi (full circle)
radius: given by pythagorean with a, b = 10, then division by 2 , we now have radius
Thus we have AoT and sector so colored region follows.
Your solutions reminds me of HSM Coxeter and also a bit of Escher, keep going. My best wishes 4 your future endeavours. Cheers!
Since it’s a right triangle, h = 10 sqrt(2) so the r of the circle is half of it or 5 sqrt(2). The area of the 2 sectors is pi*r^2/4 and subtracting that from 50 gives 11
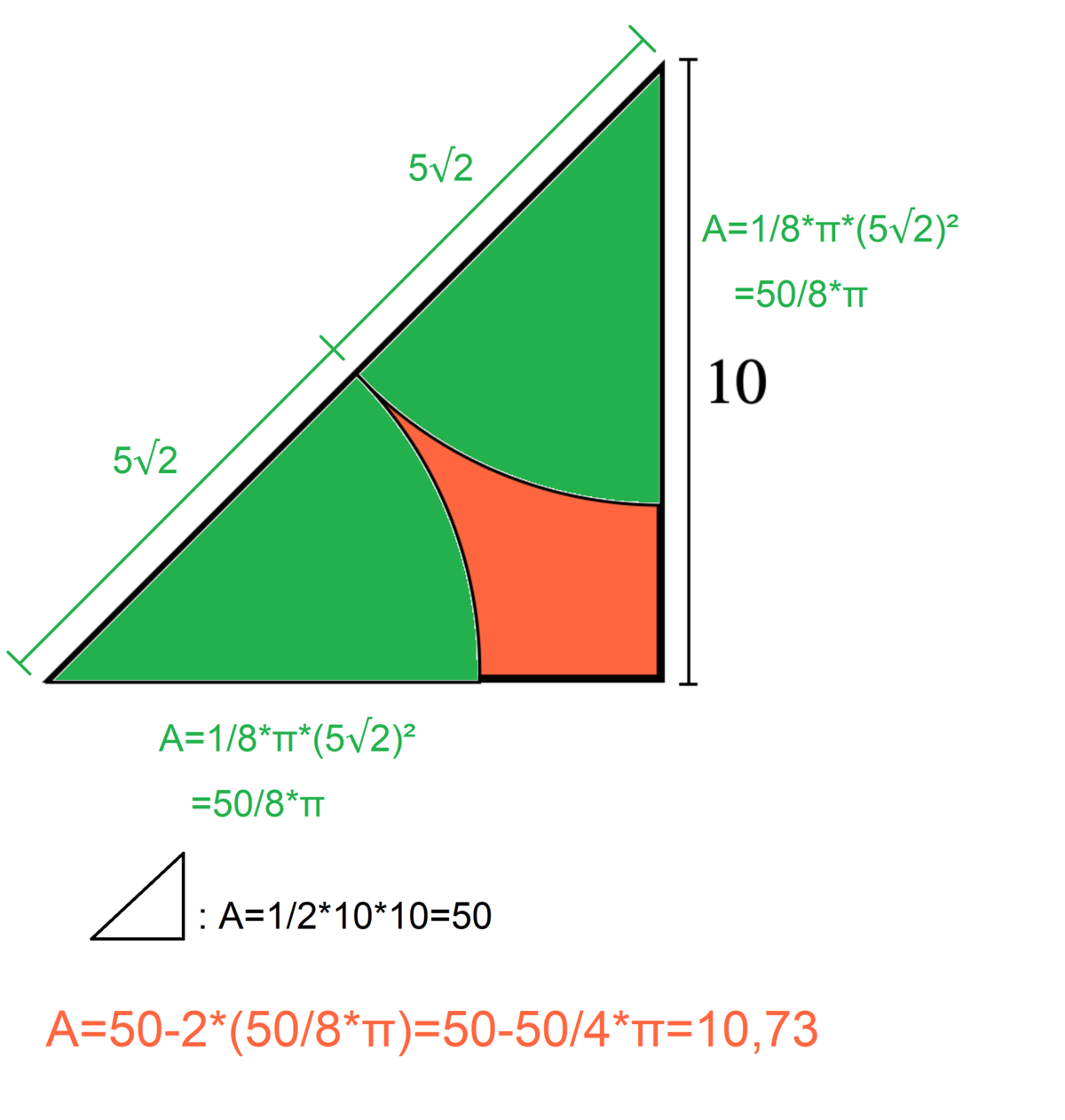
As a right isosceles with a leg of 1 0 , the triangle has acute angles of 4 5 ° and a hypotenuse of 1 0 2 , and an area of A triangle = 2 1 ⋅ 1 0 ⋅ 1 0 = 5 0 .
Just one of the sectors has a radius that is half the triangle's hypotenuse, 5 2 , a 4 5 ° central angle, and an area of A sector = 3 6 0 ° 4 5 ° ⋅ π ( 5 2 ) 2 = 4 2 5 π .
Therefore, the area of the red shape is A red = A triangle − 2 A sector = 5 0 − 2 ⋅ 4 2 5 π ≈ 1 1 .