Seductive Recursive Sequences
 (
α
n
)
and
(
β
n
)
are two sequences defined recursively as
α
n
=
2
α
n
−
1
+
1
and
β
n
=
8
β
n
−
1
+
1
with
α
0
=
β
0
=
0
.
Find the ratio
(
α
n
)
and
(
β
n
)
are two sequences defined recursively as
α
n
=
2
α
n
−
1
+
1
and
β
n
=
8
β
n
−
1
+
1
with
α
0
=
β
0
=
0
.
Find the ratio
β 6 7 2 α 2 0 1 6 .
The answer is 7.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
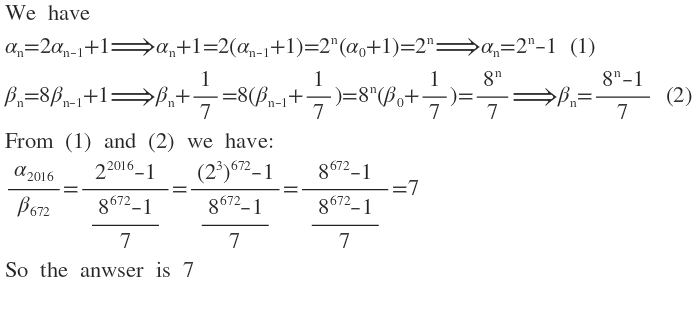
How did you replace 2(a_ n-1 + 1) with 2^n(a_0+1)?
It's easy to show using number base expansion that, in general, for a recursively defined sequence a n = x a n − 1 + 1 , a n = x − 1 x n − 1 . In this case, α n = 2 n − 1 and β n = 7 8 n − 1 . Because 6 7 2 2 0 1 6 = 3 , the fraction becomes β n α 3 n = 7 8 n − 1 2 3 n − 1 = 7 8 n − 1 8 n − 1 = 7 .
Literally my first post, so go easy on me. I'm also not much of a trained mathematician, but I've experience in doing contest questions.

α N = ∑ k = 0 N − 1 2 k = 2 N − 1
β J = ∑ k = 0 J − 1 8 k = 8 J − 1 = 2 3 ∗ J − 1
⟹ β J α N = 2 3 ∗ J − 1 7 ∗ ( 2 N − 1 )
For N = 2 0 1 6 and J = 6 7 2 ⟹ 3 ∗ J = 2 0 1 6 ⟹
β 6 7 2 α 2 0 1 6 = 7 .