Seeing diagram solves the problem
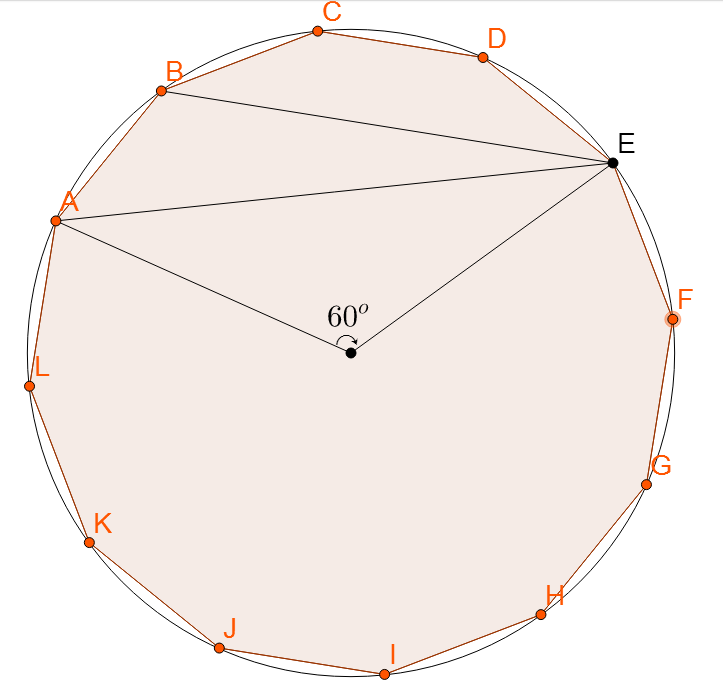
A convex polygon of twelve sides is inscribed in a circle and has in some order six sides of length and six of length . Find the integral part of the radius of the circle.
The answer is 6.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
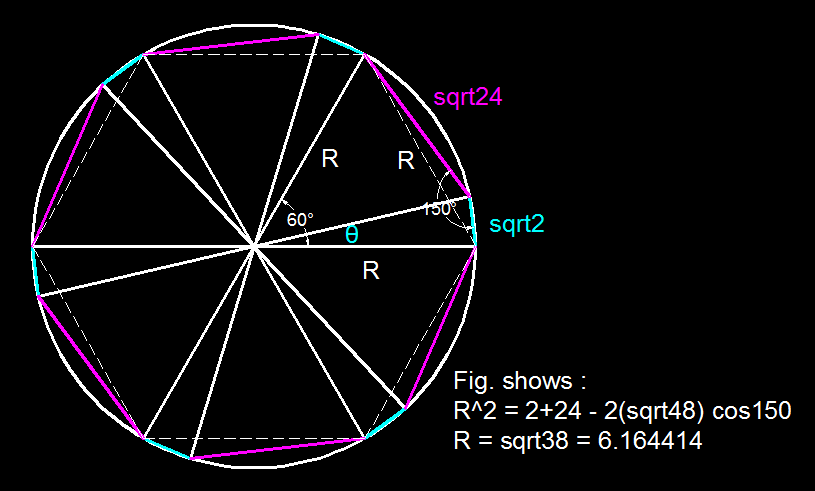
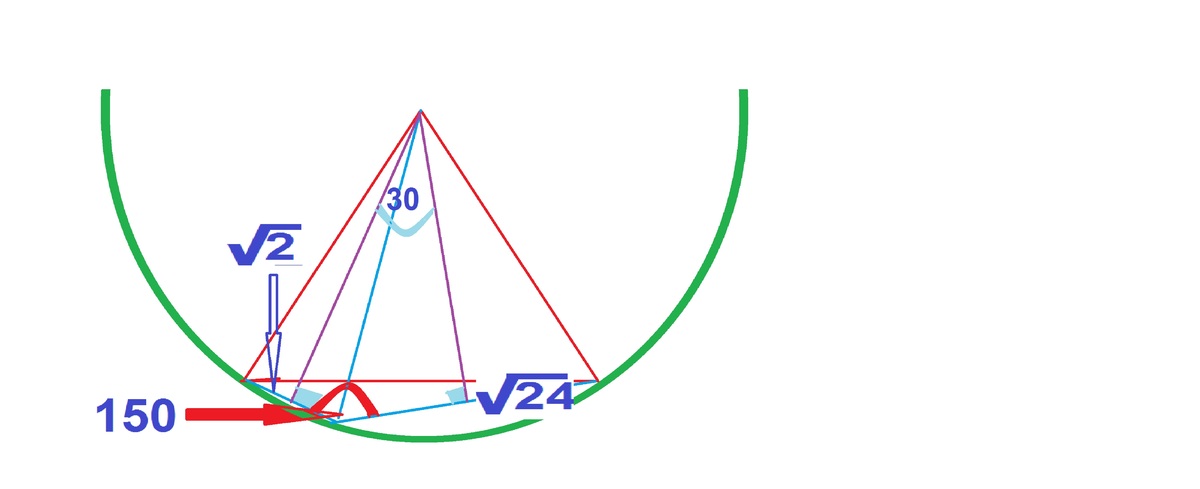
Let the angles subtended by sides of length 2 and 2 4 at the centre be α and β respectively. Then, 6 ( α + β ) = 2 π ⇒ α + β = 3 π 2 R sin 2 α = 2 2 R sin 2 β = 2 4
Now, bashing gives the result R = 3 8 .
What was the intended solution?