Seek Earth's Geography in Alg-Geometry
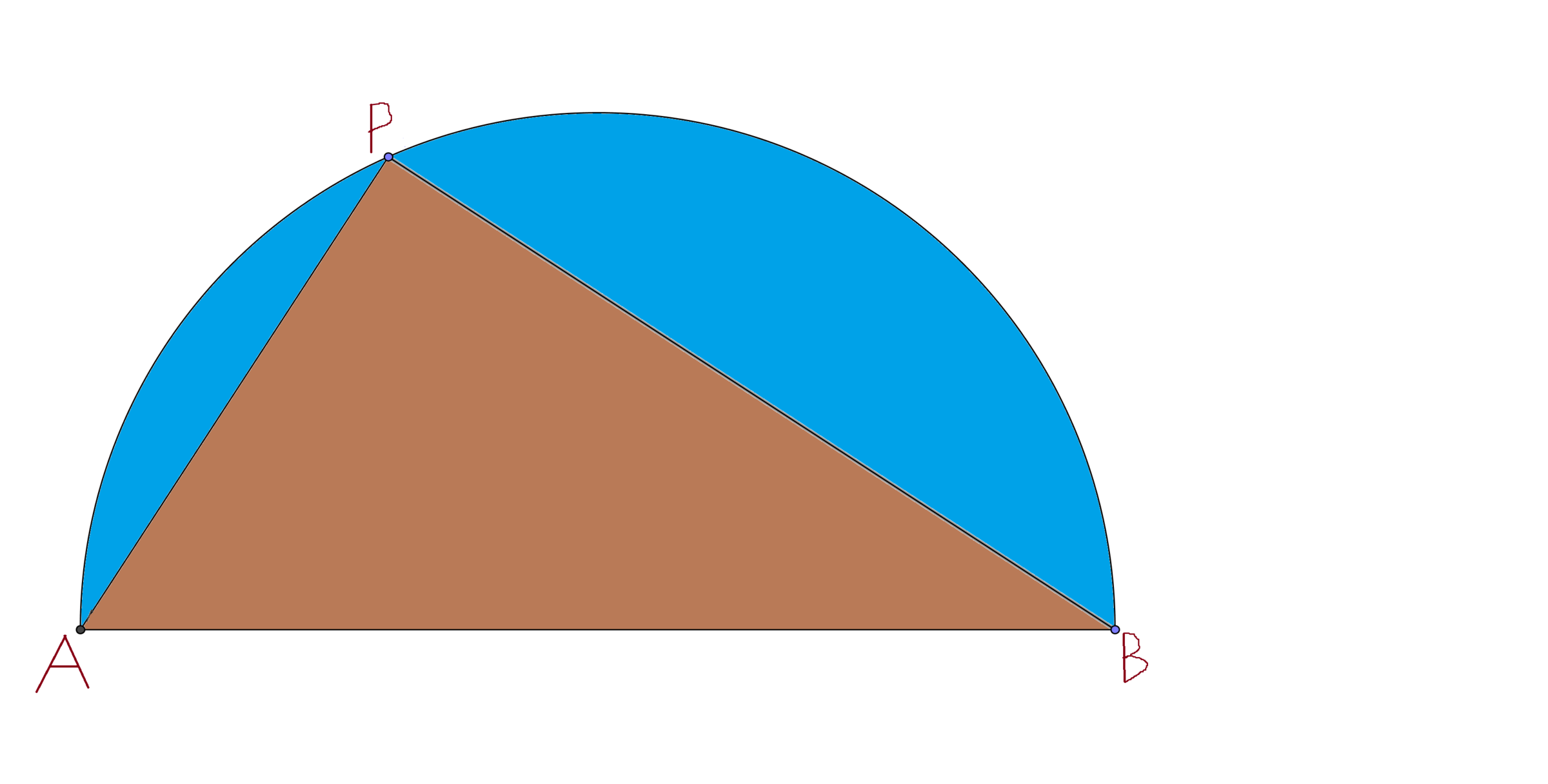
Consider a semicircle with radius r and a point P on its circumference such that P A + P B is maximum.
Then, find the area of the blue region if r = 6 3 7 0 . (Radius of earth is 6370 km)
Use the approximation π = 7 2 2 .
The answer is 23186800.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
I did not check the note and did the calculations on google, which took pi as 3.14 and ended up giving me a wrong answer >_<
@Calvin Lin I am a bit confused... This question must be Algebra or Geometryor Caculus? Since I have proved it by Algebra , there may be some Geometric proof too.Also , Chew Seong Cheong has posted a calculus solution. So I need your opinion. Thanks!
Now that we have an algebraic and a calculus solution, let me suggest a geometric solution as well, for the sake of variety.
Let t be the angle P A B . Then A P + P B = 2 r cos t + 2 r sin t = 2 2 r sin ( t + π / 4 ) . The maximum is attained when t = π / 4 , making the sine equal to 1. Now the area we seek is 2 π r 2 − 2 2 r × r ≈ 7 4 r 2 = 2 3 1 8 6 8 0 0
Thanks a lot! I needed a geometric solution. :)
It can be a Geometry problem but we must use Calculus.
We know that ∠ A P B = 9 0 ∘ . If ∠ P A B = θ , then P A + P B = l = 2 r ( cos θ + sin θ ) .
d θ d l = 2 r ( − sin θ + cos θ ) , when d θ d l = 0 ⇒ tan θ = 1 ⇒ θ = 4 5 ∘ .
We note that d θ 2 d 2 l < 0 . Therefore, P A + P B is maximum when θ = 4 5 ∘ and P A = P B = 2 r .
The area of b l u e region
A b l u e = Area of semicircle − △ A P B (when P A = P B = 2 r ) = 2 π r 2 − 2 ( 2 r ) 2 = 2 π − 2 r 2 = ( 7 1 1 − 1 ) 6 3 7 0 2 = 2 3 1 8 6 8 0 0 .
Oh my God! It can be Calculus problem too .. by your solution.
Extreme values are obtained in this symmetric conditions when PA=PB. So brown area of isosceles right triangle is 2 1 ∗ ( 2 ∗ r ) 2 , S e m i c i r c l e a r e a = 2 1 ∗ π ∗ r 2 ∴ b l u e a r e a = { 7 1 1 − 1 } ∗ 6 3 7 0 2 = 2 3 1 8 , 6 8 0 0 . .
Let P B = a , P A = b .
Since a , b > 0 , Using R . M . S inequality,
2 a + b ≤ 2 a 2 + b 2 ⇒ 2 a + b ≤ 2 ( 2 r ) 2 ⇒ 2 a + b ≤ 2 2 r 2 ⇒ a + b ≤ 2 r 2
We see that maximum is attained at equality a = b = r 2
This implies that P A + P B is maximum when Δ P A B is a 4 5 0 − 4 5 0 − 9 0 0 triangle.
Area of triangle ABC = 2 1 × r 2 × r 2 = r 2
Area of semicircle = 2 1 × 7 2 2 × r × r = 7 1 1 r 2
⇒ Required area = 7 1 1 r 2 − r 2 = 7 4 r 2
Substituting r = 6 3 7 0 gives us the area as 2 3 1 8 6 8 0 0