Seems difficult at first glance, but is it?

Geometry Level 4

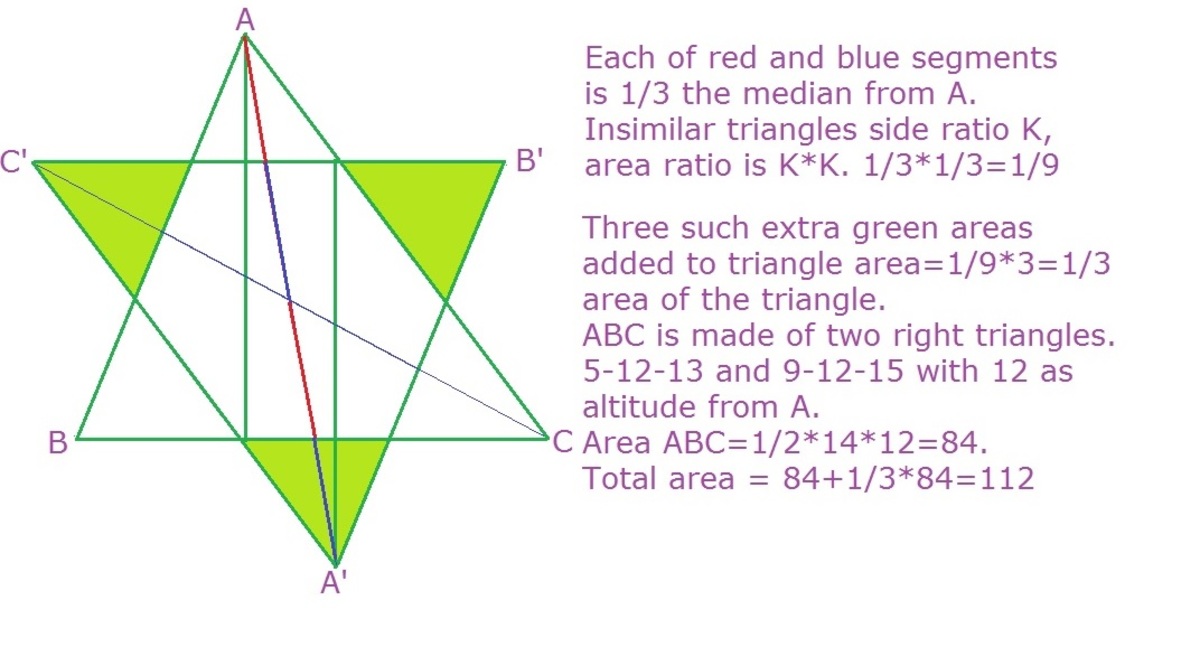
In $\triangle ABC$ , $AB=13$ , $BC=14$ , and $AC=15$ . Point $G$ is the intersection of the medians of $\triangle ABC$ . Points $A',B',$ and $C'$ are the images of points $A,B,$ and $C$ respectively after a $180^\circ$ rotation about $G$ . What is the area of the union of the two regions enclosed by the triangles $ABC$ and $A'B'C'$ ?

Extras:

This is in the set Contest Problems
This is an AIME Problem

The answer is 112.

2 solutions

Niranjan Khanderia
Oct 24, 2017

Nam Diện Lĩnh
Jul 2, 2015

When ABC is rotated, we can see that the area of the union of the two regions is equal the area of ABC plus the areas of 3 small triangles. We can easily prove that a small triangle's area is equal $\frac{1}{9}$ the area of ABC, thus the final area is $\frac{4}{3}$ the area of ABC. Using Heron's formula, the area of ABC is 84, so the answer is 112

Seems difficult at first glance, but is it?

The answer is 112.

2 solutions

0 pending reports