Segment OK?
Geometry
Level
1
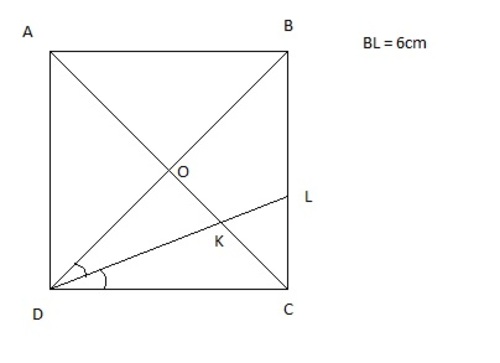ABCD is a square, AC & BD are its diagonals which intersect at O.
Given angle BDL =angle LDC, and BL = 6cm.
find the length of the line segment OK.
The answer is 3.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
In triangle BDC, applying angle bisector theorem, we get
DC / DB = CL / BL
x / x√2 = (x-6) / 6 [ x = side of the given square (in cm.)]
Solving this, we get x = 3√2 + 6 cm -----------------(1)
Now, applying angle bisector theorem in triangle ODC, we get
DC / DO = CK / OK
x / (x√2 / 2) = CK / OK [ DO = half the length of diagonal = 1/2 * x√2]
(2x / x√2) + 1 = (CK / OK) + 1
(2 + √2) / √2 = OC / OK
(2 + √2) / √2 = (x√2 / 2) / OK [OC = half the length of diagonal = 1/2 * x√2]
OK = x / (2 + √2)
OK = (3√2 + 6) / (2 + √2) [ Putting the value of x from -------(1)]
OK = 3cm