Segments in square

Simple and elegant solution here:

Consider $M$ the midpoint of the square side and $P$ de intersection point $S, R$ the vertex. $\triangle RPM$ has the same height as $\triangle RPS$ and a half from it's base , you can prove that they have same height if you notice that $45$ ◦ is the bissector from the square vertex and both are angles from the triangles too $\therefore$

$\triangle RPM$ = $\frac{\triangle RPS}{2}$ you can notice too that $\triangle RPM$ + $\triangle RPS$ its $\frac{1}{4}$ from the square since they touch the midpoint of the square $\therefore$ square area is $120$ and orange area is a half from the square - $\triangle RPM$ wich is 50 .

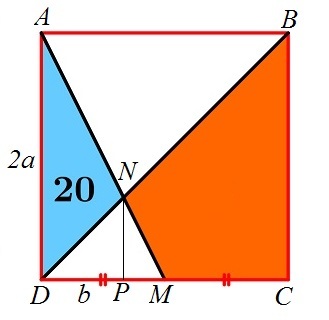
Let the square be $ABCD$ with sides $2a$ . The midpoint of $CD$ be $M$ . The line $AM$ cuts $BD$ at $N$ and the altitude from $N$ meets $CD$ at $P$ and $DP=b$ .

We note that $\triangle AMD$ is similar to $\triangle NMP$ . Therefore,

$\begin{aligned} \frac {PM}{\color{#3D99F6}NP} & = \frac {DM}{AD} & \small \color{#3D99F6} \text{Since }\angle BDC = 45^\circ, \implies NP=DP \\ \frac {PM}{\color{#3D99F6}DP} & = \frac a{2a} \\ \frac {a-b}b & = \frac 12 \\ 2a-2b & = b \\ \implies b & = \frac 23 a \end{aligned}$

Then, the area of $\triangle DMN$ , $[DMN] = \dfrac {ax}2 = \dfrac 13 a^2$ . We know that

$\begin{aligned} [ADN]+[DMN] & = \frac 12 \times a \times 2a \\ 20+\frac 13a^2 & = a^2 \\ \frac 23 a^2 & = 20 \\ \implies a^2 & = 30\end{aligned}$

We also know that

$\begin{aligned} [BCMN]+[DMN] & = \frac 12 \times 2a \times 2a \\ [BCMN]+\frac 13a^2 & = 2a^2 \\ \implies [BCMN] & = \frac 53 a^2 = \boxed{50} \end{aligned}$

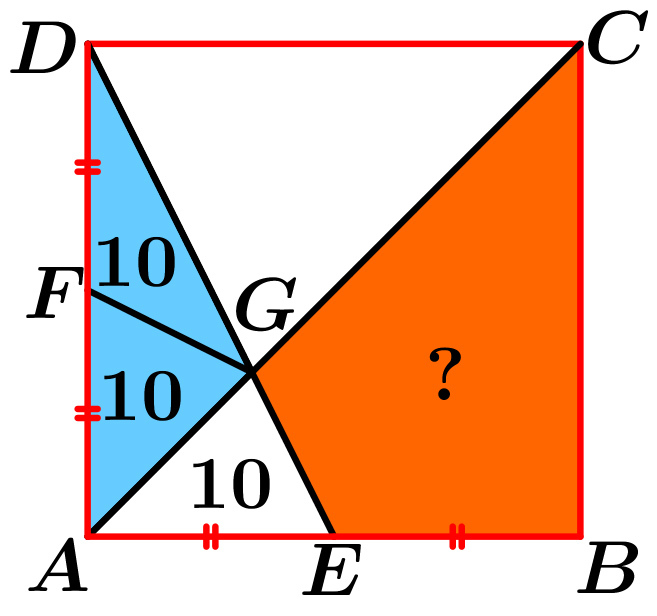
If $F$ is the midpoint of $AD$ , then $[AFG]=[FGD]=10$ . $G$ is on the $AC$ diagonal, so $GE=GF$ . From that the $\triangle AEG, \triangle AFG$ are coincident, because they have to same sides. So $[AEG]=10$ . Then

$[AED]=\dfrac{AE*AD}{2}=[AEG]+[AFG]+[FGD]=3*10=30$ $\Rightarrow [ABCD]=4[AED]=120$ $[BCGE]=[ABC]-10=\dfrac{[ABCD]}{2}-10=\dfrac{120}{2}-10=60-10=\boxed{50}$