Segments Within Rectangles
In rectangle A B C D above, whose length is twice its width, two line segments are drawn from point E to the bottom two vertices C and D . If D E bisects ∠ A E C , what is the measure, in degrees, of ∠ A E D ?
The answer is 75.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
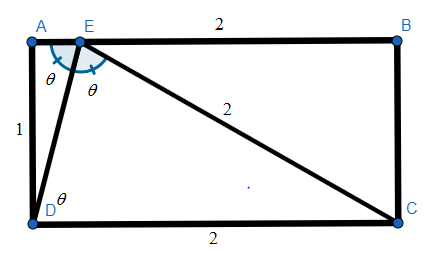 Let
A
D
=
B
C
=
1
, then
A
B
=
C
D
=
2
, and
∠
A
E
D
=
∠
D
E
C
=
θ
. Since
A
B
is parallel to
C
D
,
∠
E
D
C
=
∠
A
E
D
=
θ
and
△
C
D
E
is an isosceles triangle. Therefore,
C
E
=
C
D
=
2
.
Let
A
D
=
B
C
=
1
, then
A
B
=
C
D
=
2
, and
∠
A
E
D
=
∠
D
E
C
=
θ
. Since
A
B
is parallel to
C
D
,
∠
E
D
C
=
∠
A
E
D
=
θ
and
△
C
D
E
is an isosceles triangle. Therefore,
C
E
=
C
D
=
2
.
We note that E D = sin ∠ A E D A D = sin θ 1 . Also E D = 2 C E cos ∠ D E C = 2 × 2 cos θ . Therefore, we have:
4 cos θ 2 sin θ cos θ sin ( 2 θ ) ⟹ 2 θ θ = sin θ 1 = 2 1 = 2 1 = 1 5 0 ∘ = 7 5 ∘ Note that 2 θ > 3 0 ∘
Clue: Compute that triangle EBC is 30 60 90 triangle
Tha angle E D C is congruent to angle A E D couse segments A B and D C are parallel and D E in a trasversal. Hence angles D E C and E D C are congruent and the triangle E C D is isosceles. Consider the right triangle C B E (right in B ). It is half an equilateral triangle couse its hypotenuse E C is double the side B C . So angle B C E is 6 0 ∘ and angle C E B is 3 0 ∘ . So angle A E C is 1 5 0 ∘ , and angle A E D is 7 5 ∘ .
Let AE = r. Let <AED = t. Computing angles, we find < BCE = 2t - 90. Then in triangle AED, tan(t) = 1/r. In triangle BCE, tan(2t - 90) = 2 -r, where we have assumed the dimensions of the rectangle are 1 and 2. So sin(t)/cos(t) = 1/r, and sin(2t - 90)/cos(2t - 90) = -cos(2t)/sin(2t) = {sin^(t) - cos^(t)/(2sin(t)cos(t) = 2 - r. Substituting cos(t) = r*sin(t), and simplifying, r^2 - 4r + 1 =0, With root r = 2 - sqrt(3), then tan(t) = 1/r gives t = 75. Ed Gray]
Suppose ∣ A D ∣ = a , ∣ D C ∣ = 2 a , and ∠ A E D = ∠ D E C = θ . Then ∠ B E C = π − 2 θ . So with ∣ A E ∣ = x we have
cot ( ∠ A E D ) = cot ( θ ) = a x and cot ( ∠ B E C ) = cot ( π − 2 θ ) = a 2 a − x = 2 − a x , in which case
cot ( θ ) + cot ( π − 2 θ ) = 2 ⟹ cot ( θ ) − cot ( 2 θ ) = 2 ⟹ cot ( θ ) − 2 tan ( θ ) 1 − tan 2 ( θ ) = 2
⟹ 2 − ( 1 − tan 2 ( θ ) ) = 4 tan ( θ ) ⟹ tan 2 ( θ ) − 4 tan ( θ ) + 1 = 0 ⟹ tan ( θ ) = 2 4 ± 1 2 = 2 ± 3 .
Now clearly θ > π / 4 ⟹ tan ( θ ) > 1 , so we take the positive root, i.e., tan ( θ ) = 2 + 3 , from which we recognize that θ = 7 5 ∘ .
Note: tan ( 7 5 ∘ ) = tan ( 4 5 ∘ + 3 0 ∘ ) = 1 − tan ( 4 5 ∘ ) tan ( 3 0 ∘ ) tan ( 4 5 ∘ ) + tan ( 3 0 ∘ ) = 1 − 3 1 1 + 3 1 = 3 − 1 3 + 1 = 2 ( 3 + 1 ) 2 = 2 4 + 2 3 = 2 + 3 .
As alternate interior angles to parallel lines A B and D C , ∠ A E D ≅ ∠ C D E , and so ∠ C E D ≅ ∠ A E D ≅ ∠ C D E which means △ C E D is an isosceles triangle with C D ≅ C E .
Since we are given that C D = 2 ⋅ B C , and since C D ≅ C E , we have C E = 2 ⋅ B C . Using right triangle △ B E C , sin ∠ B E C = C E B C or sin ∠ B E C = 2 1 , which means ∠ B E C = 3 0 ° .
Finally, as a straight angle, ∠ A E B = 1 8 0 ° , and since ∠ A E B = ∠ A E D + ∠ C E D + ∠ B E C and ∠ A E D ≅ ∠ C E D , we have 1 8 0 ° = ∠ A E D + ∠ A E D + 3 0 ° , which means ∠ A E D = 7 5 ° .