Self-referential pie chart
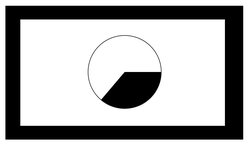 As shown in the image, there is a 10"x20" white poster with a 1 inch black border on all sides. A black and white pie chart is in the center of the poster. The radius of the pie chart is
inches.
As shown in the image, there is a 10"x20" white poster with a 1 inch black border on all sides. A black and white pie chart is in the center of the poster. The radius of the pie chart is
inches.
If the black portion of the pie chart is to accurately represent the fraction of the poster's area that is black, what angle (in degrees) should the black part of the pie chart have?
You should assume that the thin black circular outline of the pie chart contributes negligible area.
Inspired by this xkcd cartoon .
The answer is 120.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
We can express the fraction f of the poster that is black in terms of the known quantities and f itself:
f = A o u t e r f A c + A o u t e r − A i n n e r
Where A c is the total area of the pie chart, A o u t e r is the area of the entire poster, and A i n n e r is the area of the white internal rectangle inside the border.
Solving this for f , we get
f = A o u t e r − A c A o u t e r − A i n n e r
Plugging in the values
A o u t e r = 2 0 0 i n 2
A i n n e r = 1 4 4 i n 2
A c = π ( 4 π 2 ) 2 = 3 2 i n 2
We find that f = 3 1 . If a third of the circle should be black, that translates to an angle of 120°.