Semi-circle Lunes

Geometry Level 3

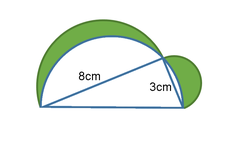A triangle is formed by connecting the two ends of the diameter of a semi-circle to a point on the circumference. Circles are constructed on the two shorter sides with diameters 8cm and 3cm respectively, so as to form two lunes (the green shaded part). Find the total area of the two lunes in cm².


The answer is 12.

Tan Chee Sen by Tan Chee Sen , 25, Malaysia

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

(Note that I use a=8 and b=3)

Take the area of the big circle: A 1 = π a 2 8 + π b 2 8 A_1 = \frac { \pi a^2 }{8} + \frac { \pi b^2 }{8}

Take the area of the triangle A 2 = a b 2 A_2 = \frac {ab}{2}

Take the sum of the areas of the little circles: A 3 = π a 2 8 + π b 2 8 A_3 = \frac { \pi a^2 }{8} + \frac { \pi b^2 }{8}

Note that A 1 = A 3 A_1 = A_3

Thus the area of the two lunes is A 3 − ( A 1 − A 2 ) = A 2 = a b 2 = 12 A_3 - ( A_1 - A_2 ) = A_2 = \frac {ab}{2} = 12

3 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...