Semi-circular Sine Wave Substitute

Calculus Level 3

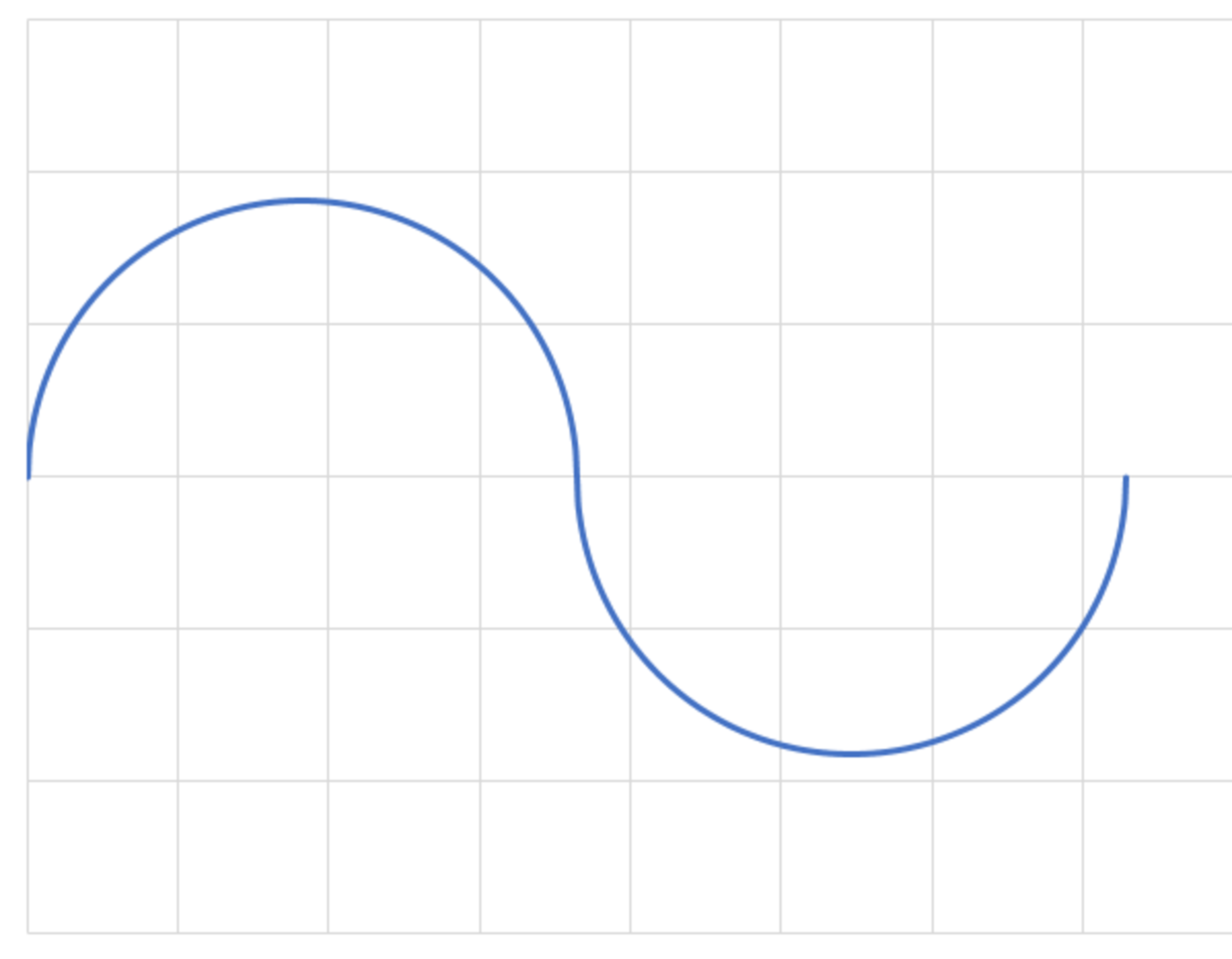
It is common knowledge that for a sine wave, the ratio of the peak value to the root mean square (RMS) value is 2 \sqrt{2} . Suppose we construct a periodic signal resembling a sine wave, composed of half circles placed end to end, with oscillating polarity.

For this signal, the ratio of the peak value to the RMS value is:

Peak RMS = A B \frac{\text{Peak}}{\text{RMS}} = \sqrt{\frac{A}{B}}

If A A and B B are positive co-prime integers, determine A + B A + B .


The answer is 5.

Steven Chase by Steven Chase , 37, USA

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Tapas Mazumdar
May 19, 2018

The radius of the circular waveform is one-fourth the time period of the wave, hence T = 4 R T = 4R . The circular waveform in terms of cartesian coordinates x x and y y can be given by

y 2 + ( x − R ) 2 = R 2 , 0 ≤ x ≤ 2 R y 2 + ( x − 3 R ) 2 = R 2 , 2 R ≤ x ≤ 4 R y^2 + (x-R)^2 = R^2 \ \ , \ \ 0 \le x \le 2R \\ y^2 + (x-3R)^2 = R^2 \ \ , \ \ 2R \le x \le 4R

Thus the RMS value for the wave can be given as

RMS value = 1 4 R ∫ 0 4 R y 2 d x = 1 4 R [ ∫ 0 2 R ( R 2 − ( x − R ) 2 ) d x + ∫ 2 R 4 R ( R 2 − ( x − 3 R ) 2 ) d x ] = 2 3 R \begin{aligned} \text{RMS value} &= \sqrt{\dfrac{1}{4R} \int_0^{4R} y^2 \,dx} \\ &= \sqrt{\dfrac{1}{4R} \left[ \int_0^{2R} (R^2 - (x-R)^2) \,dx + \int_{2R}^{4R} (R^2 - (x-3R)^2) \,dx \right] } \\ &= \sqrt{\dfrac23} R \end{aligned}

while the peak value is simply R R . Thus required ratio is 3 2 \sqrt{\dfrac32} giving the answer as 5 \boxed{5} .

2 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...