Semi-Magical Hexagon 2
If the numbers 5, 8, 9, 11, 13, 14, 15, 17, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, and 33 can be placed in the following hexagon so that the sum of the numbers in each row (in all three directions) is the same, find the number that will be placed in the center.
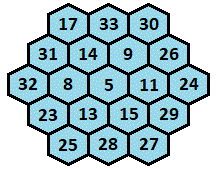
The answer is 5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Great solution!
Log in to reply
The yellow hexagons determine the values in the blue hexagons precisely (if two adjacent yellow hexagons contain the values x , y , then the opposite blue hexagon contains x + y + 5 ), and so there are only 7 arrangements of the values in the yellow hexagons that give possible solutions (no repeated values, all allowed values). It is then easy to check that only one of these allows us to fill in values in the red hexagons as well.
Log in to reply
Very nice!
Can you explain how you got that result? (The x,y therefore x+y+5 relationship)
Sum of each of 5 rows is 400/5=80. Following Magic Hexagon solution, 12 numbers from 17 to 33 are arranged in outer most ring. Arranging remaining 7 numbers from 5 to 15 is quite simple to get the solution. Center hexagon ends with number 5.
The sum of all the numbers is 4 0 0 , so this divided by the 5 horizontal rows gives a magical constant M for each row of M = 5 4 0 0 = 8 0 .
The edge rows have 3 numbers each, and the only way to make 3 of the given numbers add up to 8 0 is to use the numbers 1 5 or greater ( 1 5 , 1 7 , 2 3 , 2 4 , 2 5 , 2 6 , 2 7 , 2 8 , 2 9 , 3 0 , 3 1 , 3 2 , and 3 3 ). That's 1 3 numbers for 1 2 spots, and the sum of these 1 3 numbers is 3 4 0 . If m is the number in the list that is not in one of the edge rows, then 1 5 ≤ m ≤ 3 3 .
Let E V be the sum of the exterior cells at each vertex of the hexagon, and let E S be the sum of the exterior cells at the center of each side of the hexagon. Using 1 2 of the 1 3 numbers from above, E V + E S = 3 4 0 − m , and since each of the 6 edge rows add up to M = 8 0 , 2 E V + E S = 6 M = 4 8 0 . These two equations solve to E V = m + 1 4 0 .
Let I R be the sum of the ring of cells in the interior of the hexagon, and let I C be the number in the center of the hexagon. Since each of the 6 rows with length 4 add up to M = 8 0 , 2 E S + 2 I R = 6 M = 4 8 0 , or E S + I R = 2 4 0 . Since each of the 5 horizontal rows add up to M = 8 0 , E V + E S + I R + I C = 5 M = 4 0 0 . These two equations solve to E V + I C = 1 6 0 .
Combining E V = m + 1 4 0 and E V + I C = 1 6 0 solves to I C = 2 0 − m . Since m ≥ 1 5 , that means I C ≤ 5 , and since 5 is the smallest number available, I C = 5 .
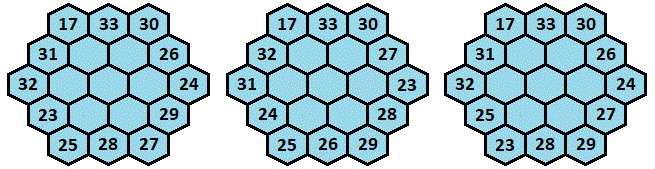
For the rest of the hexagon, since I C = 5 , then from I C = 2 0 − m we have m = 1 5 , and from E V = m + 1 4 0 we have E V = 1 5 5 . Disregarding similar rotational symmetries, there are only 3 different ways the edge rows could be filled:
Filling in 5 as the center number and x as one of the other interior cells, and using the fact that each row adds up to M = 8 0 , we can deduce the following:
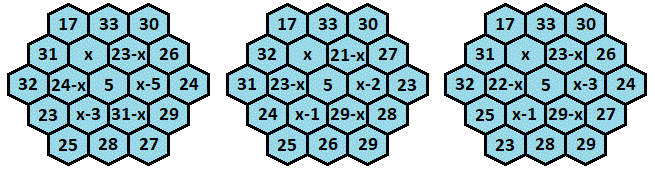
In the first case, there is an x and a 31 - x, but no two numbers 15 or less can add up to 31. In the second and third case, there is an x, 29 - x, and x - 1, and with the given numbers x = 14. However in the second case, this leads to 21 - x = 7, which is not an option. Therefore, it is the third case where x = 14, which solves to the following:
In this case we have 5 X = a + b + c + d is the sum of all the numbers, which is 4 0 0 , and hence X = 8 0 . In addition, c ≥ 5 + 8 + 9 + 1 1 + 1 3 + 1 4 = 6 0 , and hence 6 0 ≤ c = X − 2 d = 8 0 − 2 d , so that d ≤ 1 0 .
If d = 8 then 5 + 9 + 1 1 + 1 3 + 1 4 + 1 5 = 6 7 ≤ c = 8 0 − 2 × 8 = 6 4 , which is impossible. Thus d = 8 .
If d = 9 then 5 + 8 + 1 1 + 1 3 + 1 4 + 1 6 = 6 6 ≤ c = 8 0 − 2 × 9 = 6 2 , which is impossible. Thus d = 9 .
Thus d = 5 . In this case the numbers in the yellow interior hexagons must be 8 , 9 , 1 1 , 1 3 , 1 4 , 1 5 .