Semi-Magical Hexagon
If you filled each cell of the following hexagon with integers (where some are the same and some are different) so that the sum of the numbers in each row, in all three directions, is 5 0 , then find the sum of the numbers in just the pink cells.
The answer is 100.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Wow, great solution!
Bonus Follow Up: Are there a finite or infinite number of solutions for filling in the hexagon with the given parameters?
Log in to reply
This doesn't feel quite in the spirit of the problem, but I'm slightly stuck doing these on my phone with a day old baby on my lap (my excuse for any errors today!).
The quick answer is, infinitely many: since the given parameters let us have some cells with the same values, we can carry on the solution by making all edge pinks have one value, all edge blues another, etc.
The equations in the solution above can be used to parameterise all these values in terms of the central pink cell P I ; we have P E B E B I = 1 0 0 − P I = 1 0 0 + 2 P I = 5 0 − 2 P I
There are six of each of these types of cell; we just set P I = 6 k + 4 for any integer k to get a solution. For example, with P I = 4 , making all edge pinks 1 6 , all edge blues 1 8 and all interior blues 7 works.
The reason I don't consider this answer exactly in the spirit of a magic hexagon is it would be nice to find a solution (or infinitely many) with distinct entries (even consecutive integer entries) - bonus bonus question?
Well, the convex combination of any two distinct solutions would itself be a solution. So if there is more than one solution, there are infinitely many solutions.
Of course, we don't know if there is even one solution at this point. But we only have 15 constraints as opposed to 19 variables, so I'm guessing there are multiple solutions.
I also found infinite solutions (similar to Chris's method), using the following:
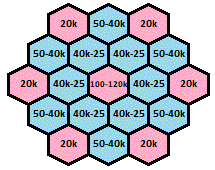
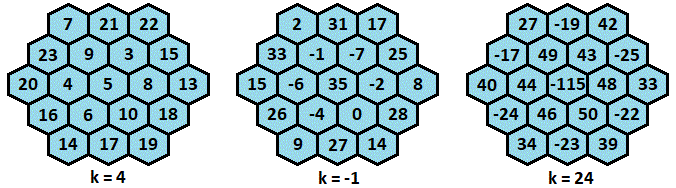
Here are some examples of all integer solutions using the above with different k values:
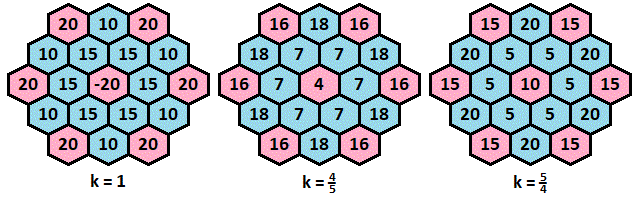
I know these are not true magic hexagons (that's why I called the problem "Semi-Magical Hexagon").
A solution with consecutive integer entries cannot exist because if x were the lowest number, than the sum of all the numbers 2 1 x ( x + 1 ) would have to add up to 2 5 0 , and this gives an irrational solution for x .
For a solution with distinct entries, you could take the magic hexagon given here and multiply each entry by 1 9 2 5 for a row sum of 5 0 . Of course, then the entries would not be integers.
I'm not sure if a solution with distinct integer entries exists.
Update: There are infinite solutions with distinct (non-consecutive) integer entries.
Combining a magic hexagon with distinct consecutive integers with a magical constant of M = 3 8 (found here ) and a semi-magical hexagon similar to the above with a magical constant of M = 1 2 gives a generator for a semi-magical hexagon with a magical constant of M = 5 0 :
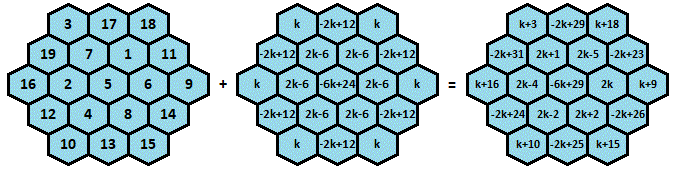
This generator gives distinct entries for k ≤ − 1 , k ≥ 2 4 , and k = 4 . Here are a few examples:
There are five disjoint horizontal rows, each of which sums to 50. Thus the sum of all entries in the hexagon is 250.
Now consider the blue hexes. The blue hexes are composed of the union of six four-hexagon rows. (There is a triangle with a horizontal base on top laying over a triangle with a horizontal base on bottom.) Each row sums to 50, thus the six rows sum to 300.
Each blue hex is in exactly two of these six rows. Thus the sum of the six rows is twice the sum over the blue hexes. I.e., the blue hexes sum to 150.
The sum of the pink hexes = the sum of all hexes - the sum of the blue hexes = 250-150 = 100.
Nice solution!
Denote by P E the sum of the six pink cells on the edge of the hexagon, P I the value of the pink cell in the interior, and similarly B E and B I for the blue cells.
Each row sums to 5 0 . Summing all six rows of length 3 , we find 2 P E + B E = 3 0 0 .
Rows of length 4 give 2 B E + 2 B I = 3 0 0 .
The three rows of length 5 give P E + 3 P I + B I = 1 5 0 .
Adding the first and third of these equations, and subtracting half the second gives 3 P E + 3 P I = 3 0 0 , so the total of the pink cells is P E + P I = 1 0 0 .