Semicircle

Geometry Level 3

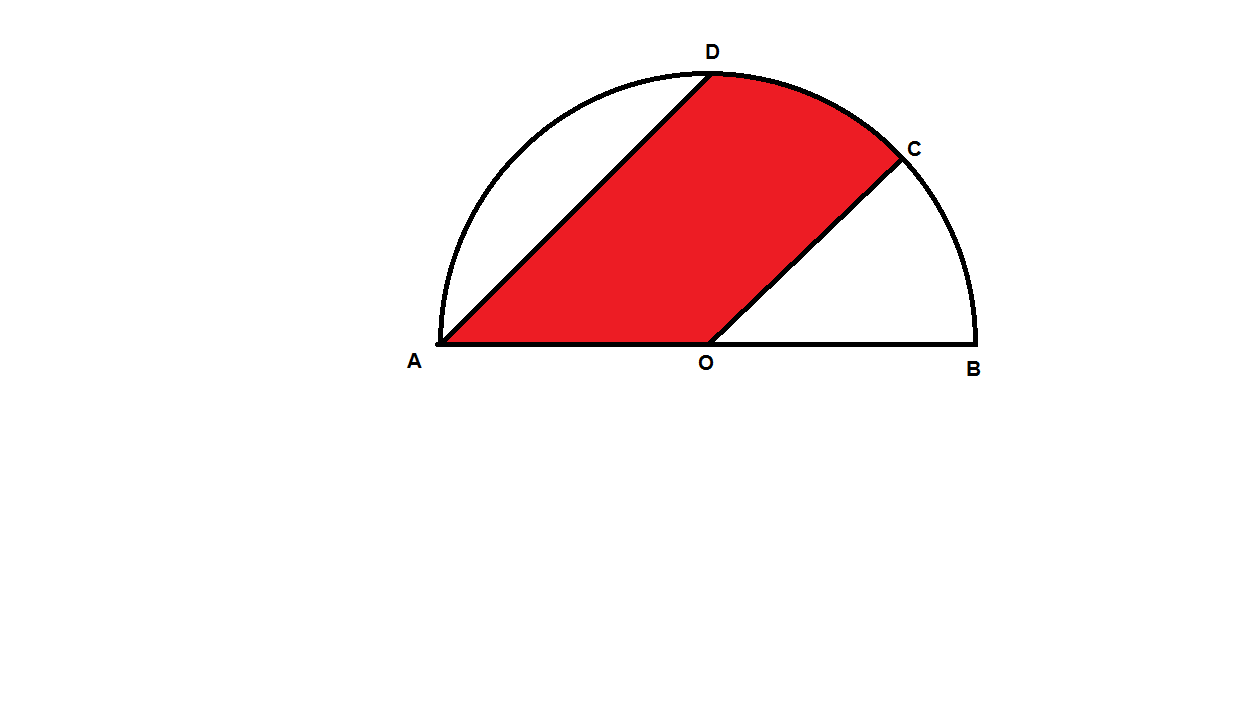
Two parallel straight lines $OC$ and $AD$ are drawn inside a semicircle of radius $r$ , such that the $\angle COB = 45^{\circ}$ where $O$ is the centre of the original circle, ( i.e mid point of $AB$ ). If the area of the red region is $\dfrac{ r^{2}(π + m)}{n}$ , where $m, n$ are positive integers , find $mn$ .

The answer is 32.

1 solution

Aziz Alasha
Oct 7, 2017

It can be easily shown that the line OD is perpendicular to the diameter AB, hence angle COD = 45 degrees .

red area = area of secor COD + triangle AOD = $\frac{ π }{8}$ $r^2$ + $\frac{ 1 }{ 2 }$ $r^2$ = $r^2$ ( $\frac{ π + 4 }{ 8 }$ )

mn = 4 * 8 = 32

why is r provided? :P

Md Zuhair - 3 years, 8 months ago

Haha good question, since the answer is the same for every r.

Peter van der Linden - 3 years, 8 months ago

Thank you mr. Peter

In fact the required area A is a a function of r , A = f(r) , so whatever the value of r is , the answer will be the same .

Aziz Alasha - 3 years, 8 months ago

Thank you Mr. md zuhair.

In fact the required area A is a a function of r , A = f(r) , so whatever the value of r is , the answer will be the same .

Aziz Alasha - 3 years, 8 months ago

Semicircle

The answer is 32.

1 solution

0 pending reports