Distance Between Intersection Points
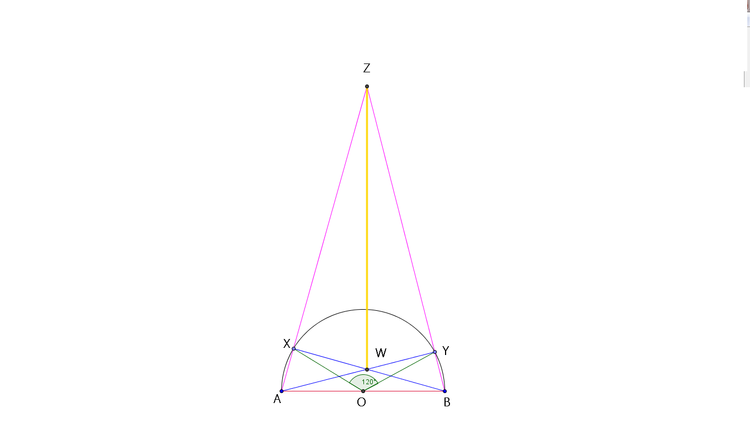 On a semicircle with diameter
A
B
and centre
O
points
X
and
Y
are chosen such that
∠
X
O
Y
=
1
2
0
∘
. Let
A
X
and
B
Y
meet at
Z
and
A
Y
and
B
X
meet at
W
. If
A
B
=
5
3
, find
W
Z
.
On a semicircle with diameter
A
B
and centre
O
points
X
and
Y
are chosen such that
∠
X
O
Y
=
1
2
0
∘
. Let
A
X
and
B
Y
meet at
Z
and
A
Y
and
B
X
meet at
W
. If
A
B
=
5
3
, find
W
Z
.
The answer is 15.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Another Solution for this .Join XY . Since angle AXB and AYB are semicircular so ang.AXB=angle.AYB=90 .Therefore Quad.ZXWY is concyclic ,hence ang.XZW=ang.XYW but ang.XYW=ang.XYA=ang.XBA (angle on the same segment) . So Tri. XZW is similar to Tri.XBA ,So XA/XW=AB/WZ also ang.XAW=ang.XOY/2=60 Therefore XA/XW=1/root3=5root3/WZ so WZ=5root3*root3=15
WXZ is a right triangle, so the hypotenuse is equal to the diameter
thank you
WZ=OZ -OW =OA tanOAZ - OA tanOAW =OA(tan1/2BOX - tan 1/2BOY) =OA(tan 0.5 150 - tan0.5 30) =5*root(3)/2( tan 75 - tan 15 ) =15 Answer
Considering symetrical segment..
It is clear that angle ZXW = angle ZYW = 90 (since AB is diameter) therefore, XWYZ is cyclic
Let angle AYO be x and BXO be y. Therefore, OAY=x(isoceles triangle AOY) and OBX=y(isoceles triangle OBX)
angle BOY=2*BAY=2x and XOA=2y
Thus, x+y=30 (since 2x+2y+120=180)
Now, angle XWY=120+x+y=150
Applying sine law in XOY(an isoceles triangle since OX=OY=r), we get XY/sin120 = OX/sin30 which gives XY=7.5
Further, Applying sine law in ZXY, we get XY/sin30=2R(where R is the radius of the circumcircle) Thus 2R=15 and since the circumcircle is also the circumcircle of WXZ(since WXZY is cyclic), therefore 2R=WZ=15.
Without loss of generality, assume that X and Y are equidistant from AB. Then angle YOB=30 and O Y = 2 5 3 . Let the altitude from Y to AB intersect AB at point G. Notice that △ Y O G is a 30-60-90 right triangle. Therefore, Y G = 4 5 3 and G O = 4 1 5 . From this, we deduce that G B = 2 5 3 − 4 1 5 . Then, by similarity of triangles, we have 4 5 3 Z O = 2 5 3 − 4 1 5 2 5 3 = 2 5 3 − 4 1 5 8 7 5 = 2 0 3 − 3 0 7 5 = 4 3 − 6 1 5 = 1 2 6 0 3 + 9 0 = 2 1 0 3 + 1 5 .
We now need to subtract WO in order to obtain WZ. Again, we use similar triangles. A G Y G = A O W O 4 5 3 W O = 2 5 3 + 4 1 5 2 5 3 = 2 5 3 + 4 1 5 8 7 5 = 2 0 3 + 3 0 7 5 = 4 3 + 6 1 5 = 1 2 6 0 3 − 9 0 = 2 1 0 3 − 1 5 .
When we subtract WO from ZO, we have 2 1 0 3 + 1 5 − ( 1 0 3 − 1 5 ) = 2 3 0 = 1 5
You cannot assume that X and Y are equidistant from A B . Its only a special case. You have to consider the more genral case. Full credit will not be given if this assumption is made.. perhaps. Maybe the staffs can say something here.
The assumption that X and Y are equidistant from A B doesn't preserve generality.
We join X , Y . Note that ∠ A X B = ∠ A Y B = 9 0 ∘ and X O , Y O are the medians of the right angled triangles A X B and A Y B . Let ∠ X B O = α and ∠ Y A O = β . Thus ∠ O X B = α and ∠ X Y A = α . Similarly ∠ Y X B = β = ∠ Y A B . Thus α + β = 3 0 ∘ .
Now if we assume that A O = X O = Y O = B O = x , then law of cosines in △ X O Y yields X Y = x 3 .
Now note that ∠ W X Z = ∠ W Y Z = 9 0 ∘ and hence W X Z Y is cyclic, W Z being the diameter of the circumscribing circle. . Thus ∠ X Z Y = ∠ X Z W + ∠ W Z Y = ∠ X Y W + ∠ W X Y = α + β = 3 0 ∘ . Therefore ∠ X W Y = 1 5 0 ∘ . Now Sine rule in △ X W Y yields
sin ∠ X W Y X Y = 2 R = W Z
or, sin 1 5 0 ∘ x 3 = W Z
or, 2 × x 3 = W Z
or, 2 x × 3 = W Z
or, W Z = 3 A B = 3 × 5 3 = 1 5