Semicircle inscribed in a square
Let be a unit square. What is the area of the largest semicircle that can be inscribed inside it?
If your answer is of the form , where , and are integers and is square-free, write your answer as .
The answer is 7.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
link text
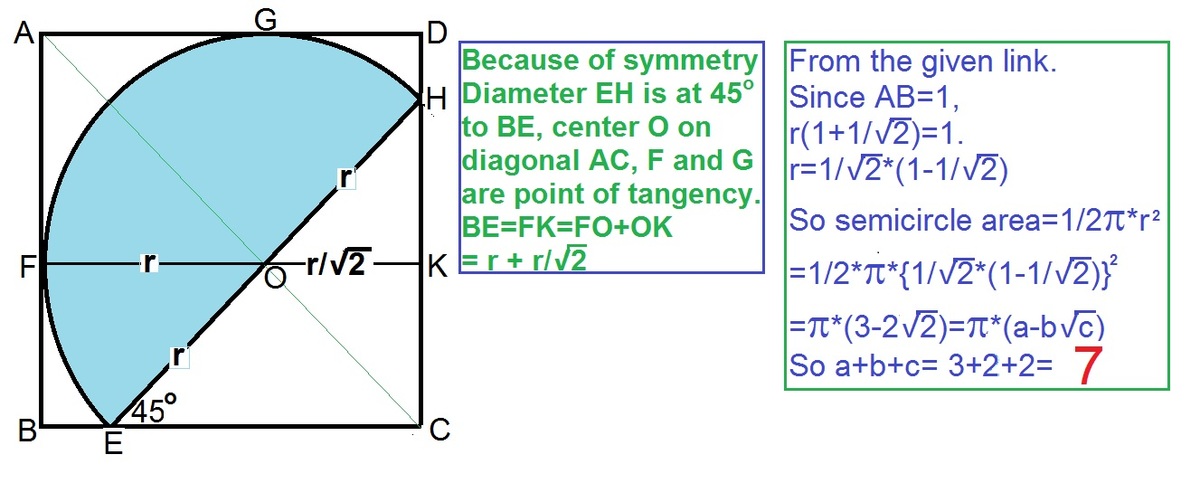
The ends of such a semi-circle will touch to a pair of adjoining sides BC, CD symmetrically at E ,H
and the other pair AB, AD tangentially at F, G.
So the diameter EH will be parallel to the diagonal BD and the center on the other diagonal AC. The sketch taken from the link and solution is due to the link given above.