Semicircles and spiral
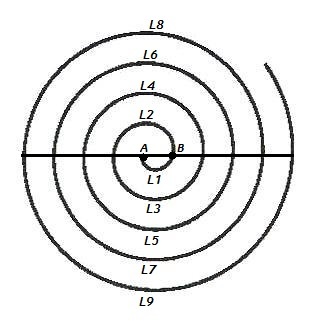 A spiral is made up of successive semicircles, with centres alternately at A and B, starting with centre at A, of radii 0.5 cm, 1.0 cm, 1.5 cm, 2.0 cm, . . . as shown in the image.
A spiral is made up of successive semicircles, with centres alternately at A and B, starting with centre at A, of radii 0.5 cm, 1.0 cm, 1.5 cm, 2.0 cm, . . . as shown in the image.
What is the total length of such a spiral made up of thirteen consecutive semicircles?
Details and Assumptions:
☻Take π = 22/7
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Discussions for this problem are now closed
As we can see in the succession that the description of the problem presents, if the radii of a semicircle is \Nu , the radii of the next semicircle will be \Nu +0.5 cm Now, to know what is the measure of a semicirle is 2 2 π r = π r Now making the sum of all the semicircles, will be 1 π ( 0 . 5 ) + 2 π ( 0 . 5 ) + 3 π ( 0 . 5 ) + . . . + 1 3 π ( 0 . 5 ) = π [ 1 ( 0 . 5 ) + 2 ( 0 . 5 ) + 3 ( 0 . 5 ) + . . . + 1 3 ( 0 . 5 ) ] = π { 0 . 5 [ 1 + 2 + 3 + 4 + . . . + 1 3 ] } = π { 0 . 5 [ 2 1 3 ( 1 4 ) ] } = 7 2 2 [ 2 1 ( 2 1 8 2 ) ] = 2 8 4 0 0 4 = 143㎝
I COULD NOT UNDERSTAND
dude this is a spiral..... there arent any semi circles..... it has formula e^theta or so.... u gotta integrate.... not just do it like this.... your answer is wrong....
What?Seriously you are gonna integrate in simple Arithmetic Progression problem that just involves knowing the formula for the circumference of a circle.
All spirals are just concentric circles with varying radii & alternating centre points of circle. Read my explanation which is almost similar to Max's way.
By using s=r x, where r is radius and x is the angle in radians Sum(s)= sum(r x) Since the angle is constant which is π.. Sum(s)=π*sum(r) By factorizing 0.5 Sum(s)=(1/2)(22/7)(1+2+...+13) (1+2+...+13)= (13)(14)/2=91 Sum(s)= (1/2)(22/7)(91)=143
Anuj mudi...you are wrong using formula is just enough..we dont need to do integration..
All of the spiral spokes are semi circles. So the formula that we should be using to get the Length of a semi-circle (Spiral) is [Circumference of Circle (read Full Circle) / 2] i.e. (22/7*radius).
Now there are 13 semi circles with radii increment with 0.5 cm (i.e. 0.5, 1, 1.5 .... 6.5).
So the total length of all the semi-circles (spiral) is [(0.5 2/7) + 1 22/7 + 1.5 22/7 + ..... 6.5 22/7]. This now becomes simple AP by removing 0.5*22/7 (1+2+3+....13).
The answer is (0.5 22/7) * ((13 14)/2). Solving it as 143.
Simply the sum of 13 terms of the AP (0.5,1,1.5...)multiplied by 22/7(not pi).So we have