Semicircles On A Line
Geometry
Level
1
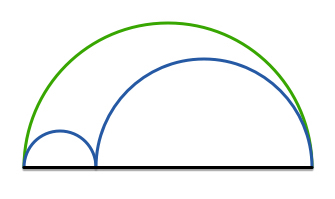
The above shows 3 semicircles on a line.
Which has a larger perimeter?
Green semicircle
Blue semicircles
Equal length
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Relevant wiki: Circles - Circumference
Let the radius of the green semicircle be R and the radius of the smaller (or if they are equal, then one of them) blue be r
Then:
• the radius of the bigger blue semicircle is R − r
• the length of the green line (the perimeter of the green semicircle) is: R π
• the perimeter of the smaller blue semicircle is: r π .
• the perimeter of the bigger blue semicircle is: ( R − r ) π .
• the length of the blue line: r π + ( R − r ) π = r π + R π π − r π = R π .
Hence, our answer is:
Equal Length .