Semicircles
In the image above there are two tangent semicircles. The side length of the square is 36cm.
What is the length of the radius of the yellow circle? Give your answer in cm .
The answer is 12.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
7 solutions
Bro how do u know that it passes through the point of touch ;
Log in to reply
they are both semicircles,so two sides of the rectangle are the diameter of both circle.
Since the shortest length between center and the arc of the circle is the radius and the shortest length between two points is always a straight line, the connection line between two tangent circle's centers will always go through the intersection and will be both radii summed up together.
Thank you.
same way like you
The radius of the large semicircle, R , is equal to D / 2 = 1 8 . Let the radius of the small semicircle be denoted by r .
The radii of both semicircles would meet at the point of intersection of the semicircles and form a straight angle. This line segment will form the hypotenuse of our right triangle, and is equal to 1 8 + r .
Using the Pythagorean theorem, we construct our right triangle in the bottom left-hand corner: ( 3 6 − r ) 2 + 1 8 2 = ( 1 8 + r ) 2 .
Expansion yields: 3 2 4 + 1 2 9 6 − 7 2 r + r 2 = 3 2 4 + 3 6 r + r 2 .
Simplifying and isolating for r reveals that r = 1 2 .
It's a quite simple problem.
It can be done with the help of the Pythagoras theorem.
Let the radius of smaller circle be x.
Let the centre of the yellow circle be O and the centre of the blue circle be O'.
Let the left corner of the of the square in which the blue circle is touching be A.
Therefore OAO' is a right triangle where
OA= 36-x
AO'= 18(radius of the blue circle)
OO' = x + 18 ( it will be a straight line since the circles are tangent to each other. The radius x and the radius 18 will both be perpendicular to the tangent and therefore form a straight line.)
Now by just applying the Pythagoras theorem.
(36-x)^2 + 18^2 = (x+18)^2
And x comes out to be 12.
I made an image so that u could understand what I am trying to say better. But it wasn't uploading. So I hope u found this useful.
Put the origin at the bottom left hand of the box. Then the equation of the blue circle is ( x − 1 8 ) 2 + y 2 = 1 8 and the equation of the yellow circle is x 2 + ( y − 3 6 + r ) 2 = r 2 where r is the radius of the yellow circle. Next we can solve for the value of r that yields only 1 solution (since the circles are tangent); if we restrict 0<r<36, then this value is unique, with all other values of r yielding 0 or 2 solutions. (r=36 also yields a tangency)
I only guesstimated. Small circle covers 2/3 of the side. The side is 36 cm long. Divide by 3 and get 12.the circle length/diameter is 24, so half of that is 12 cm.
Let A is the centre of the yellow circle, B is the centre of the blue circle, C is the point of tangency and D is the point at the bottom left of the square. => A, B, C are aligned. Let x is the radius of the yellow circle. => AD²+BD²=AB²=(AC+BC)² => (36-x)²+18²=(x+18)² => x²-72x+36²+18²=x²+36x+18² => 108x=1296 => x=12cm => The area of the yellow semi-circle is S=½πx²=72π (cm²).
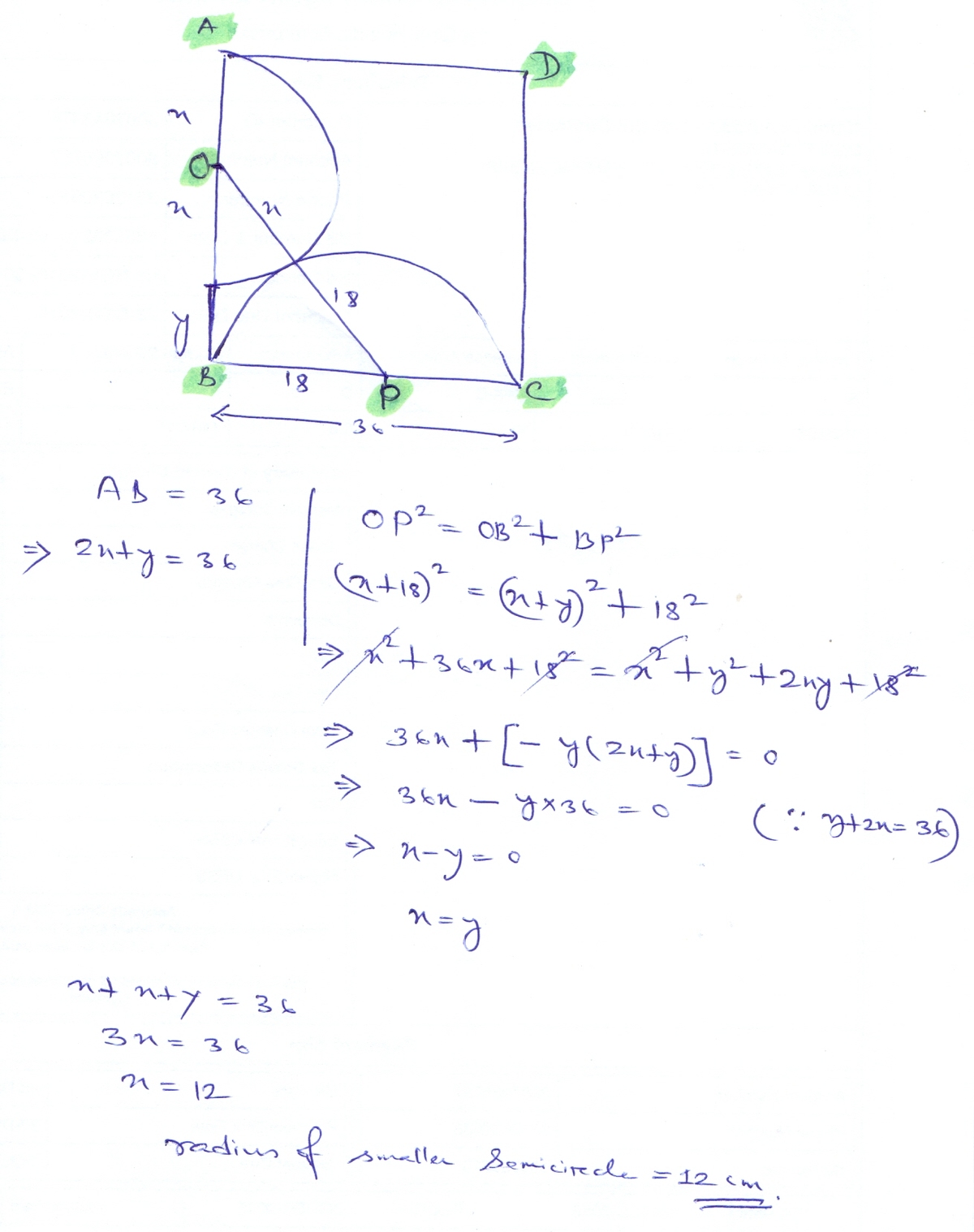
then using Pythagoras theorem:
(r+18)^2 = (36-r)^2 + (18)^2
r^2 + 2(18)r +18^2 = [ (36)^2 -2(36)r +r^2] +(18)^2
r^2 + 36r +18^2 = (36)^2 - 72r +r^2 +18^2
cancelling like terms,
36r = 36^2 - 72r
108r = 36 X 36
r = 12