SEND MORE MONEY..
Number Theory
Level
4
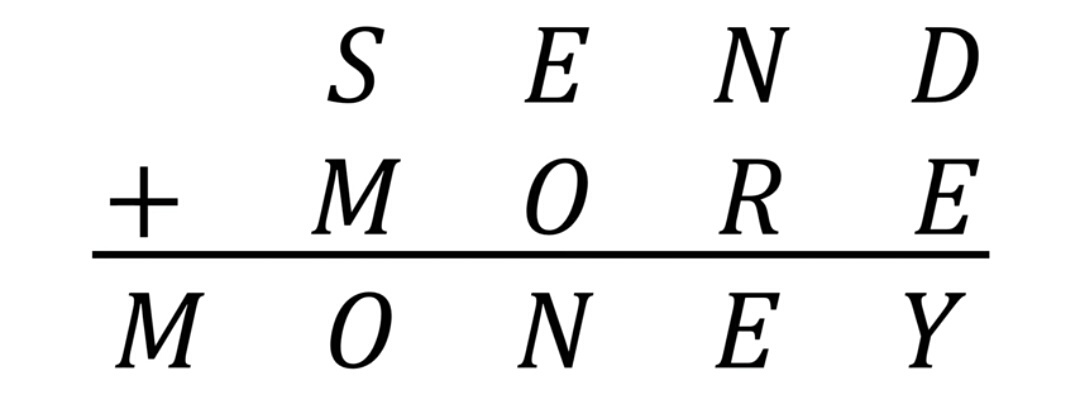
What is the sum of the value of all distinct letters?
Note:
- Each letter is a distinct digit.
- and the solution is unique.
The answer is 38.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Relevant wiki: Algebra Warmups - Cryptograms
In the above addition problem, each letter represents a different digit. Break the code so that the resulting numbers add up correctly.
M is obviously 1, since there is no way there can be carryover than one when only two digits are added. Similarly, O must be zero and S either 8 or 9. A quick check shows that if S = 8 , E must be equal to 9 , and N will equal 0. But this is impossible because O = 0 . So S = 9 , making the result so far:
9 E N D + 1 0 R E = 1 0 N E Y .
Since E plus zero plus carry over equals N , it follows that N = E + 1 and that N + R > 9 , there must be a carryover, or N + R = E + 1 0 , if there is no carryover from the first column; on the other hand, if there were a carryover, we would have N + R = E + 9 . Substituting for N its equivalent value E + 1 in these last two equations gives E + 1 + R = 1 0 and E + 1 + R = E + 9 or R = 9 or 8 .
Since S = 9 , R must equal 8 and E + D = 1 2 or more (there must be a carryover and the digits 0 and 1 have already been assigned). Therefore, the only possible values for E , D , and N are 5 , 6 , and 7 .
N = E + 1 and E + D = 1 2 or more ⟹ E = 5 , N = 6 , D = 7 and Y = 2 ⟹ S E N D + M O R E = M O N E Y ⟺ 9 5 6 7 + 1 0 8 5 = 1 0 6 5 2
Therefore, sum of digits is: 9 + 5 + 6 + 7 + 1 + 0 + 8 + 2 = 3 8