Separating two superconducting rings
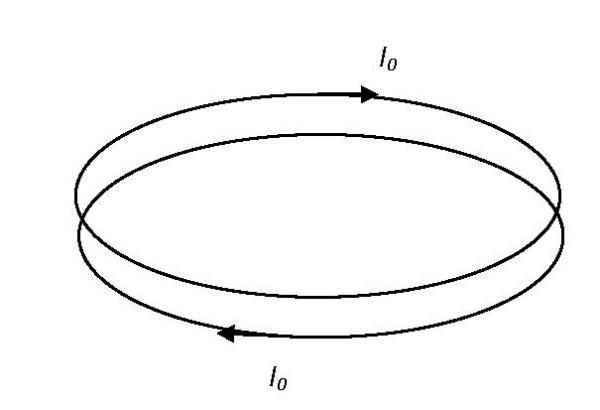
Two identical superconducting rings are brought very close to each other (see the image below). The currents in the rings are equal to
I
0
=
0
.
0
5
A
.
Determine the the current
I
1
in Amps
in the rings if we separate them far apart.
The answer is 0.1.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Since the rings are superconducting, the induced emf is zero and therefore the flux through each ring must be constant. That is,
E
=
I
R
=
0
implies
E
=
−
d
t
d
Φ
=
0
(Faraday's Law). Now, the flux through a ring must be proportional to its own current. We have that
Φ
=
L
I
where the proportionality coefficient is called self-inductance. Note that because the rings are close to each other, the flux through one of the rings in the initial configuration is
Φ
0
=
L
I
0
+
L
I
0
=
2
L
I
0
.
The final flux equals for that ring is
Φ
1
=
L
I
1
.
Comparing the last two expressions, we obtain
I
1
=
2
I
0
=
0
.
1
A
.
When we separate two identical superconducting rings far apart, there are two magnetic field vectors tend to the same side. So that, sum vector is greater than the first one 2 times. Thus I = 2 I 0 = 0 . 1 A
Since the ring is superconducting, the emf in the ring equal to IR is always zero and unchanged. Thus the total flux through it is a constant. When the two currents are very close to each other, the flux through one ring can be considered to be caused by one ring conducting the two currents ,i.e 2 I o . When one ring is taken apart very far, the magnetic flux is caused only by its own current. To make the flux unchanged, the current now is 2 I o = 0 . 1 A