Septic Sums
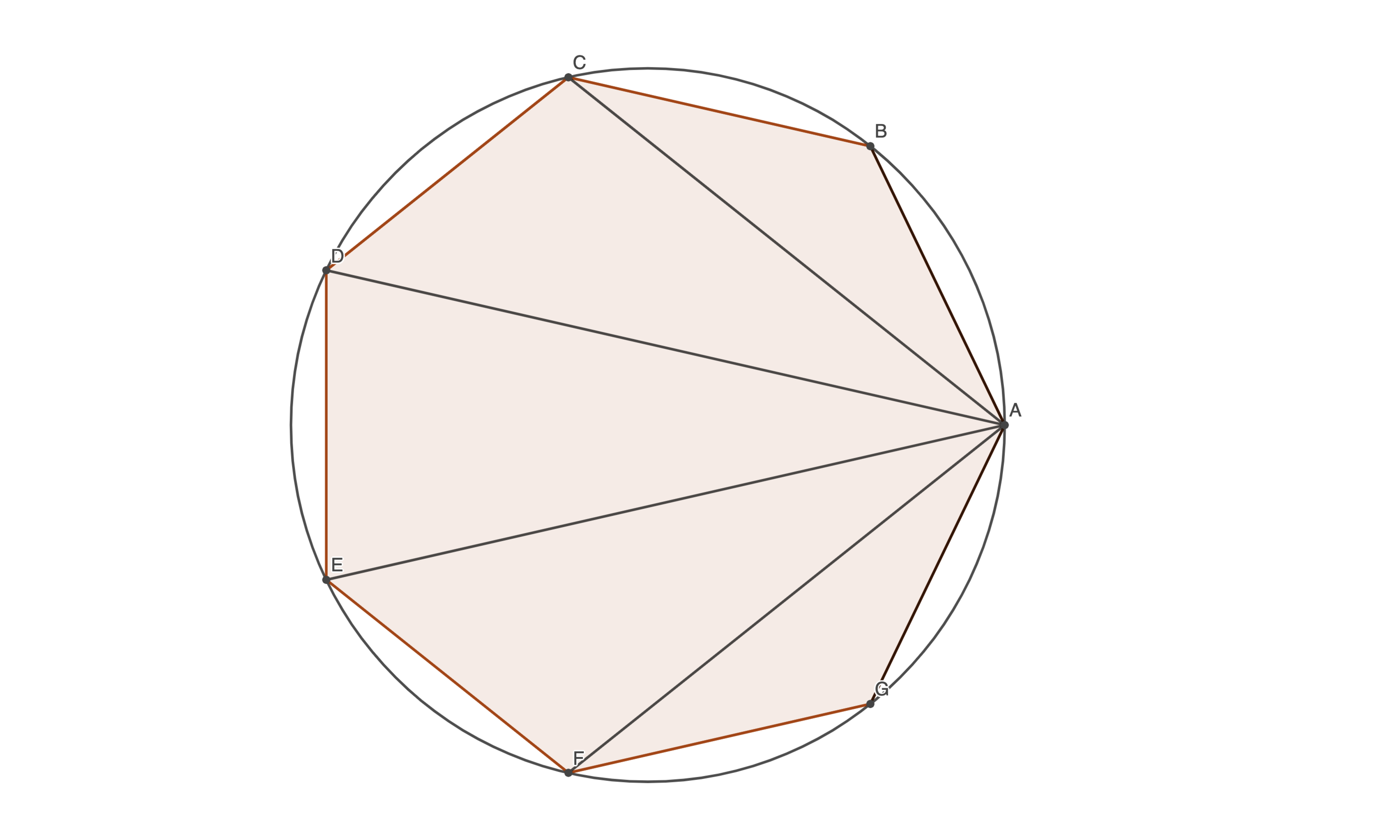
A regular heptagon is inscribed in the unit circle. What is the value of A B 4 + A C 4 + A D 4 + A E 4 + A F 4 + A G 4 ?
The answer is 42.0.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Instead of A , B , C , D , E , F , G , label the vertices Z j for 0 ≤ j ≤ 6 . If z = e 7 2 π i , for 0 ≤ j ≤ 6 , then Z j represents z j on the Argand diagram, and so j = 1 ∑ 6 Z j Z 0 4 = j = 1 ∑ 6 ∣ ∣ z j − 1 ∣ ∣ 4 = j = 1 ∑ 6 ( 2 − z j − z − j ) 2 = j = 1 ∑ 6 ( 4 + z 2 j + z − 2 j − 4 z j − 4 z − j + 2 ) = 3 6 + j = 1 ∑ 6 ( z 2 j + z − 2 j − 4 z j − 4 z − j ) = 4 2 + j = 0 ∑ 6 ( z 2 j + z − 2 j − 4 z j − 4 z − j ) = 4 2
Fine problem. N=6,7,8,9,10,11... S(N)=36,42,48,54,60,66...
True (and obvious by generalising the expression @Mark Hennings gave for the sum).
Let O be the center of the unit circle. By cosine rule , we have A B 2 = O A 2 + O B 2 − 2 ⋅ O A ⋅ O B ⋅ cos 7 2 π = 2 ( 1 − cos 7 2 π ) ⟹ A B 4 = 4 ( 1 − cos 7 2 π ) 2 . Similarly, A C 4 = 4 ( 1 − cos 7 4 π ) 2 and A D 4 = 4 ( 1 − cos 7 6 π ) 2 . Then the sum of the six terms is:
S = 8 ( ( 1 − cos 7 2 π ) 2 + ( 1 − cos 7 4 π ) 2 + ( 1 − cos 7 6 π ) 2 ) = 8 ( 3 − 2 ( cos 7 2 π + cos 7 4 π + cos 7 6 π ) + cos 2 7 2 π + cos 2 7 4 π + cos 2 7 6 π ) = 8 ( 3 − 2 ( − 2 1 ) + 2 1 ( 3 + cos 7 4 π + cos 7 8 π + cos 7 1 2 π ) ) = 8 ( 4 + 2 1 ( 3 − ( cos 7 3 π + cos 7 π + cos 7 5 π ) ) ) = 3 2 + 4 ( 3 − 2 1 ) = 3 2 + 1 0 = 4 2