Septic Triangle

Geometry Level 5

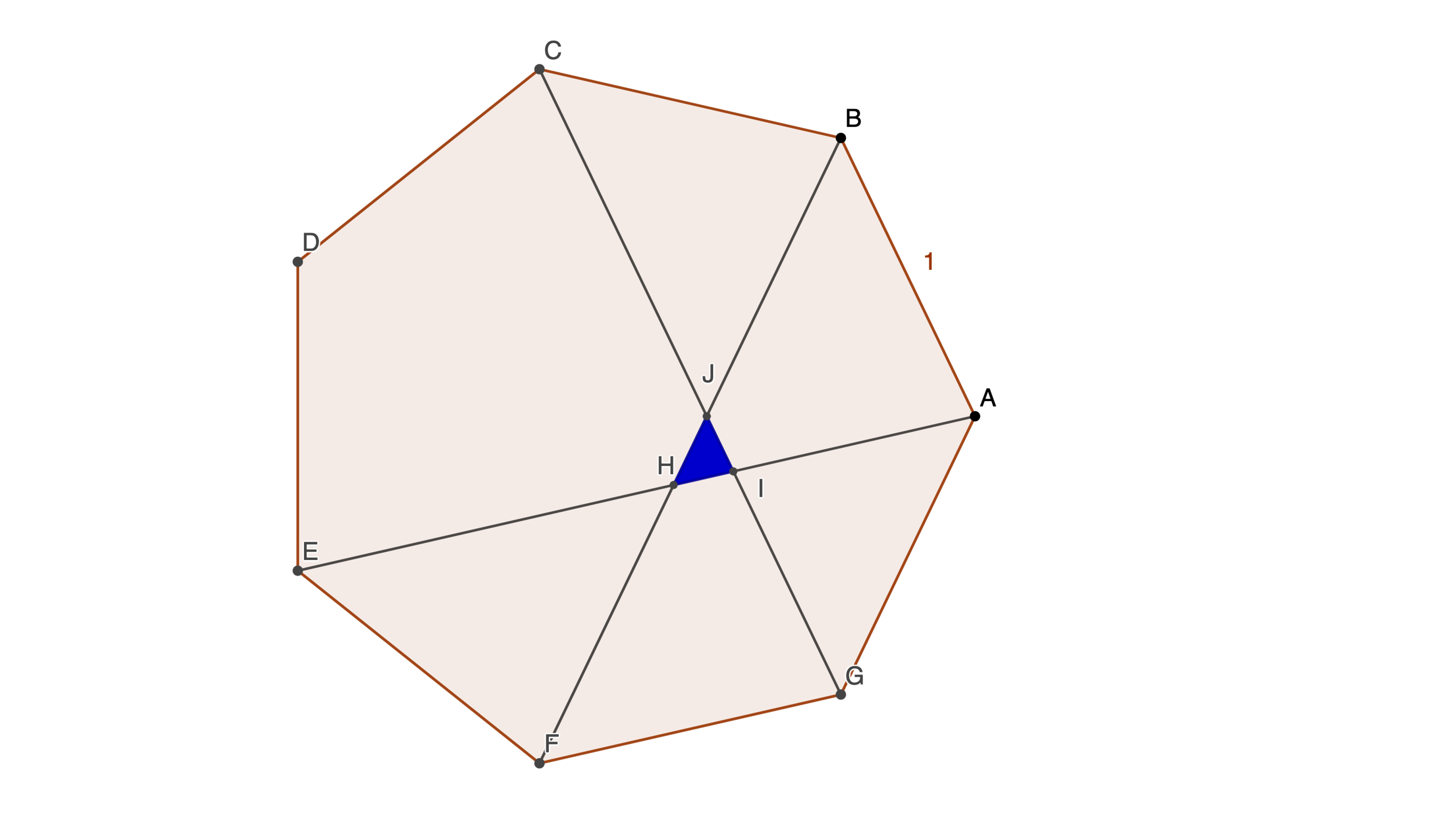
The figure shows a regular septagon with side length 1. △ H I J \triangle HIJ is formed by diagonals A E , B F AE, BF , and C G CG . What is the area of △ H I J \triangle HIJ ? Find a closed-form solution, convert it to a decimal number, and submit the sum of the first 50 digits to the right of the decimal point.


The answer is 239.

Fletcher Mattox by Fletcher Mattox , 72, USA

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

Yuriy Kazakov
Mar 10, 2021

Find Area - use WolframAlpha

Find sum digits

Answer - 239.

0 Helpful 0 Interesting 1 Brilliant 0 Confused

How did you get x + y = 1 x+y=1 ?

Fletcher Mattox - 3 months ago

JI=y, IG=x, BJGA - rhombus. BJ=x+y=GA=1

Yuriy Kazakov - 3 months ago

Aha! Nice observation. Thank you.

Fletcher Mattox - 3 months ago
Fletcher Mattox
Mar 9, 2021 
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
 
# Find the area of the smallest triangle in a fully connected unit heptagon
# https://www.geogebra.org/classic/rehfw2tx
# https://brilliant.org/problems/septic-triangle/

from math import isclose
from sympy import *

radius =  csc(pi/7)/2                   # arrange for side length = 1
center = Point(0,0)                     # centered at Origin
p = Polygon(center, radius, n=7)
side = trigsimp(p.sides[0].length)
assert(isclose(side, 1, abs_tol=1e-100))

A,B,C,D,E,F,G  = p.vertices
AE = Line(A, E)
GC = Line(G, C)
BF = Line(B, F)
H = AE.intersection(GC)[0]
J = AE.intersection(BF)[0]
I = GC.intersection(BF)[0]
area = Triangle(H, I, J).area
print(area)
N_area = N(area, 60)
print(N_area)
s_area = str(N_area)
digits = s_area[2:52]
digit_sum = sum(list(map(int, digits)))
print(digit_sum)


1
2
3
 
(-cos(3*pi/14) + cos(pi/14))*(-789*cos(2*pi/7)/(8*sin(pi/7)) - 789*sin(3*pi/14)/(8*sin(pi/7)) - 385*sin(pi/14)/(4*sin(pi/7)) - 15*sin(5*pi/14)/(4*sin(pi/7)) - 15*(1 - cos(2*pi/7))**2*cos(2*pi/7)/sin(pi/7) - 23*(1 - cos(2*pi/7))**2*sin(pi/14)/sin(pi/7) - 3*(1 - cos(2*pi/7))**2*sin(3*pi/14)/sin(pi/7) + 9*(1 - cos(pi/7))**2/(2*sin(pi/7)) + 43*cos(3*pi/7)/(8*sin(pi/7)) + 2*(1 - cos(3*pi/7))**2/sin(pi/7) + 35*(1 - cos(2*pi/7))**2/(4*sin(pi/7)) + 10*(1 - cos(2*pi/7))**2/tan(pi/7) + 36/tan(pi/7) + 901/(8*sin(pi/7)))/(32*(sin(2*pi/7) + 2*sin(pi/7))*(-sin(pi/7) + sin(2*pi/7) + cos(pi/14))*(-6*cos(pi/14) + 5*sin(pi/7) + 4*cos(3*pi/14))*sin(pi/14)*sin(pi/7)**2)
0.0191225580385579541933490594070239691892793864506960823994008
239

1 Helpful 1 Interesting 1 Brilliant 0 Confused

The area is 4 sin ⁡ 3 ( π 14 ) sin ⁡ ( π 7 ) \boxed{4 \sin^3\big(\tfrac{\pi}{14}\big) \sin\big(\tfrac{\pi}{7}\big)} and this is 0.0191225580385579541933490594070239691892793864506960823994007897861099600100983419092024586714785028599944956629719990953621880...

Peter Csorba - 3 months ago

Don´t you think that 50 digits is a bit too much when this is a geometry question. Because I got the correct answer, but my calculator could not give me 50 digits after decimal point.

Dan Czinege - 3 months ago

Yes, it was a bit immature of me. On the other hand, there is no excuse for letting precision stop you from answering the question assuming you have a closed-form expression. Just use Wolfram Alpha or any other online calculator.

Fletcher Mattox - 3 months ago

What do think about this - link text

Yuriy Kazakov - 3 months ago

Log in to reply

Nice! You are a man after my own heart.

Fletcher Mattox - 3 months ago

Well, I did not think of using Wolfram Alpha. At least I learned I can use it to calculate my answers with higher precision than calculator on my computer. :)

Dan Czinege - 3 months ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...