Sequence!
n = 0 ∑ ∞ ( n + 1 ) ( n + 2 ) ( n + 3 ) ( n + 4 ) 1 = X 1 , X = ?
The answer is 18.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
This is a better way for solution.
Really very impressive method. Congratulations.
Nice solution sir. ⌣ ¨
I kinda cheated though. I wrote a C++ program to find the value. :D
telescopic method! nice one
Your 2nd and 3rd lines are some thing I never thought of . Thanks for adding to my knowledge.
Integration is easier than telescoping, I guess. Though, I will contradict with that one because one has to take 4 times integration of one thing only.
E
x
p
.
=
∑
0
∞
(
n
+
1
)
(
n
+
2
)
(
n
+
3
)
(
n
+
4
)
1
=
∑
2
∞
(
n
−
1
)
n
(
n
+
1
)
(
n
+
2
)
1
S
p
l
i
t
i
n
g
i
n
t
o
p
a
r
t
i
a
l
f
r
a
c
t
i
o
n
s
E
x
p
.
=
∑
2
∞
6
(
n
−
1
)
1
−
∑
2
∞
6
(
n
+
2
)
1
−
∑
2
∞
2
n
1
+
∑
2
∞
2
(
n
+
1
)
1
.
.
.
.
(
1
)
1
s
t
t
e
r
m
f
r
o
m
(
1
)
.
.
.
.
∑
2
∞
6
(
n
−
1
)
1
=
∑
2
4
6
(
n
−
1
)
1
+
∑
5
∞
6
(
n
−
1
)
1
.
l
a
s
t
t
e
r
m
f
r
o
m
a
b
o
v
e
∑
5
∞
6
(
n
−
1
)
1
=
∑
2
∞
6
(
n
+
2
)
1
=
−
2
n
d
t
e
r
m
f
r
o
m
(
1
)
a
n
d
3
r
d
t
e
r
m
f
r
o
m
(
1
)
−
∑
2
∞
2
n
1
=
−
∑
2
2
2
n
1
−
∑
3
∞
2
n
1
.
l
a
s
t
t
e
r
m
f
r
o
m
a
b
o
v
e
∑
3
∞
2
n
1
=
−
∑
2
∞
2
(
n
+
1
)
1
=
−
4
t
h
t
e
r
m
f
r
o
m
(
1
)
a
n
d
E
x
p
.
r
e
d
u
c
e
s
t
o
,
E
x
p
.
=
∑
2
4
6
(
n
−
1
)
1
−
∑
2
2
2
n
1
E
x
p
.
=
6
1
∗
(
1
+
1
/
2
+
1
/
3
)
−
2
1
∗
2
1
=
1
8
1
1
8
Sanjeet Raria's method is out of the box and much better, but I gave the method above as the normal method. I made finding partial fraction a little easy by shifting the summation starting at 0 to one starting at 2. I have not shown how to find partial fraction assuming that, that can be done with out difficulty.
( n + 1 ) ( n + 2 ) ( n + 3 ) ( n + 4 ) 1 = ( n + 1 1 − n + 2 1 ) ( n + 3 1 − n + 4 1 )
= 6 ( n + 1 ) 1 − 2 ( n + 2 ) 1 + 2 ( n + 3 ) 1 − 6 ( n + 4 ) 1
So we have 6 1 − 2 ∗ 2 1 + 2 ∗ 3 1 − 6 ∗ 4 1
+ 6 ∗ 2 1 − 2 ∗ 3 1 + 2 ∗ 4 1 − 6 ∗ 5 1
+ 6 ∗ 3 1 − 2 ∗ 4 1 + 2 ∗ 5 1 − 6 ∗ 6 1 + . . .
= 6 ∗ 3 1 = 1 8 1 so X = 1 8 .
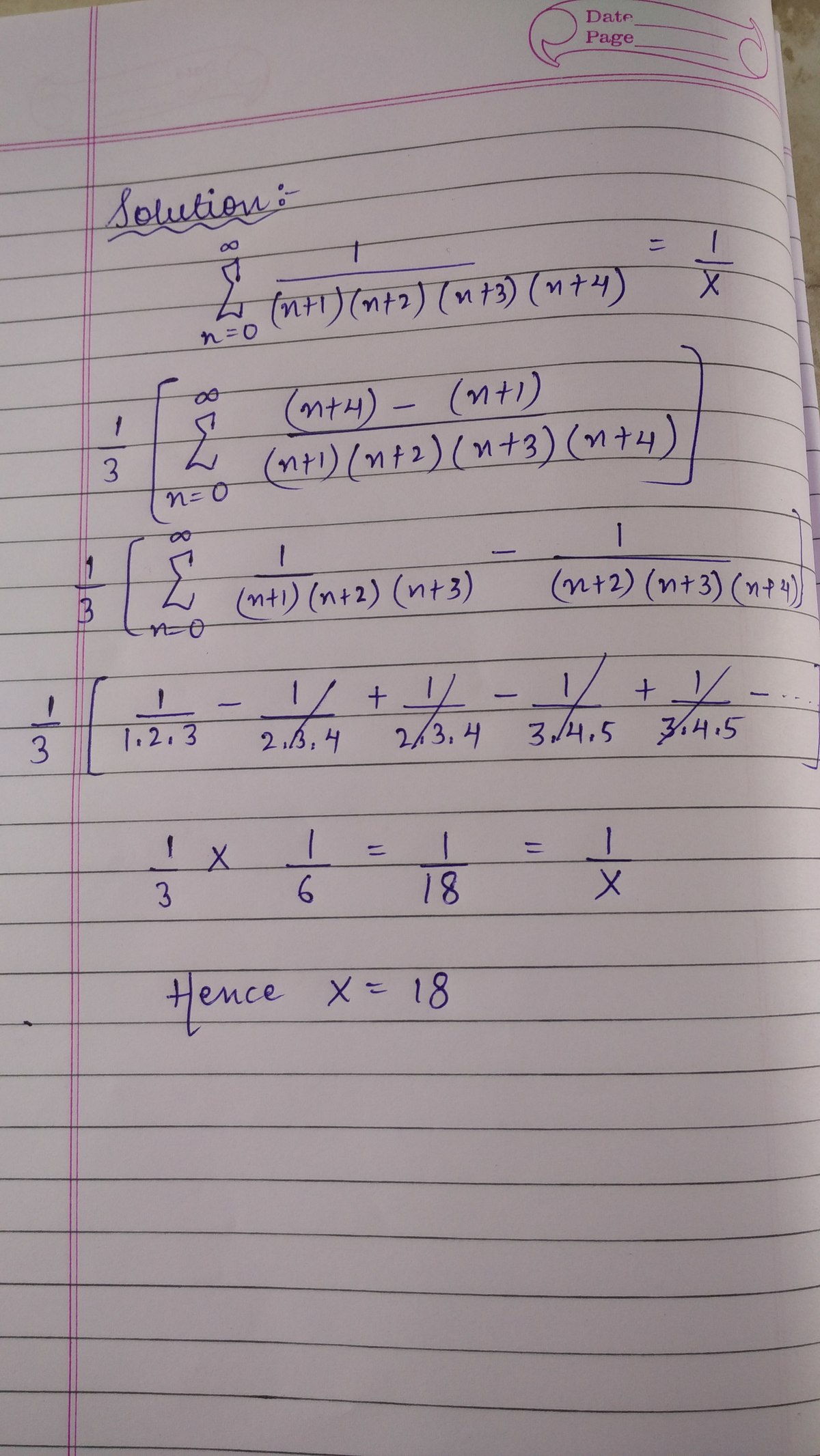
Considering ( n + 1 ) ( n + 2 ) ( n + 3 ) ( n + 4 ) 1 = 3 1 ( ( n + 1 ) ( n + 2 ) ( n + 3 ) 1 − ( n + 2 ) ( n + 3 ) ( n + 4 ) 1 ) = 3 1 ( f ( n ) 1 − f ( n + 1 ) 1 ) , f ( n ) = ( n + 1 ) ( n + 2 ) ( n + 3 ) The required expression is now equal to = n = 0 ∑ ∞ 3 1 ( f ( n ) 1 − f ( n + 1 ) 1 ) = 3 1 [ ( f ( 0 ) 1 − f ( 1 ) 1 ) + ( f ( 1 ) 1 − f ( 2 ) 1 ) + + + + ∞ t e r m s = 3 1 [ f ( 0 ) 1 − ∞ 1 ] = 3 1 • f ( 0 ) 1 = 3 1 • 1 • 2 • 3 1 = 1 8 1
Hence answer is 1 8
One can even generalize this idea to get the sum any number of terms