Sequence in sequence of sequences

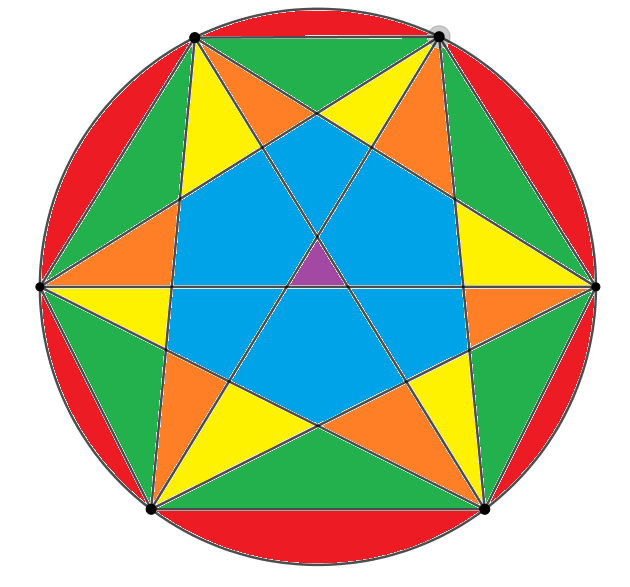
Let $n$ be the number of points on the circle and $R$ be the number of separated regions. Although $R = 2^{n - 1}$ holds true for positive integers $n$ from $1 \leq n \leq 5$ , it is not true for $n \geq 6$ . The number of points $n$ and the number of regions $R$ are actually related by the equation

$R = 1 + {n \choose 2} + {n \choose 4}$

$1$ for the starting region of the circle, ${n \choose 2}$ for the number of possible chords that can be drawn (each new chord adds a new region), and ${n \choose 4}$ for the number of possible quadrilaterals that can be drawn (each new quadrilateral has two intersecting diagonals that adds a new region).

In this problem, the fifth process would have $n = 6$ points on the circle, for $R = 1 + {6 \choose 2} + {6 \choose 4} = 1 + 15 + 15 = \boxed{31}$ regions.

---

Note : The equation $R = 1 + {n \choose 2} + {n \choose 4}$ is also equivalent to $R = \frac{n^4 - 6n^3 + 23n^2 - 18n + 24}{24}$ .

There are a total of 31 divided areas with 6 starting points on the circle.