Sequences in Geometry
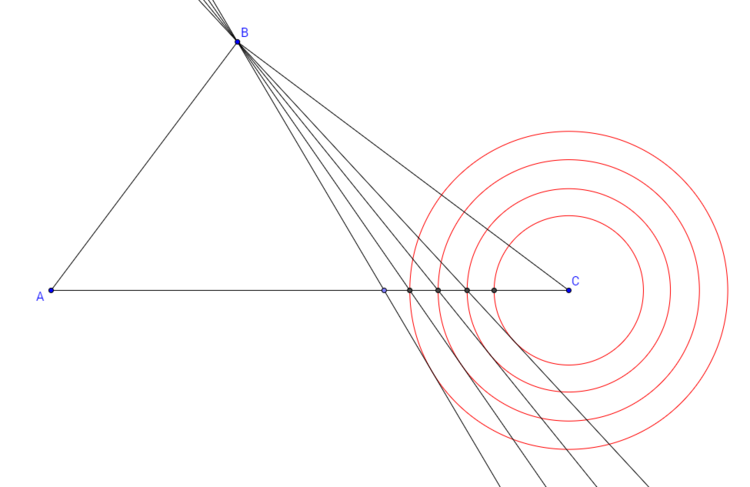 Triangle
is such that
,
, and
. For all integers
,
Triangle
is such that
,
, and
. For all integers
,
- Let be some point on between and such that is not an altitude.
- Let be the line through and .
- Let be the circle with center tangent to .
- Let be the radius of .
- Let be the intersection of with between and .
These sequences of geometric figures can be seen in the diagram above, with the labels removed. (The diagram is finite, but the sequences are infinite.)
The sequence of real numbers , for all integers , satisfies this recurrence relation:
for some positive integers . Find .
The answer is 597.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Next, we find an equation for l n + 1 . It goes through B and P n + 1 , so we use the point-slope formula for the equation of a line: y − y 1 = m ( x − x 1 ) . We'll let the point be P n + 1 , and the slope is
m = − 5 1 6 + r n 5 1 2 − 0 = 5 r n − 1 6 1 2 .
Putting this all together, we have that the equation for l n + 1 is
y − y 1 y y = m ( x − x 1 ) = 5 r n − 1 6 1 2 ( x + r n ) = 5 r n − 1 6 1 2 x + 5 r n − 1 6 1 2 r n .
Multiplying 5 r n − 1 6 by both sides and rearranging, we get the standard form equation:
1 2 x − ( 5 r n − 1 6 ) y + 1 2 r n = 0 .
To find r n + 1 , we just find the distance from C to l n + 1 . To do this, we use a formula for the distance from a point to a line. The distance between the point ( p , q ) and the line A x + B y + C = 0 is
A 2 + B 2 ∣ A p + B q + C ∣ .
Since C is the origin, the numerator of this is just ∣ C ∣ . Plugging in using our equation for l n + 1 , we get
r n + 1 = A 2 + B 2 ∣ C ∣ = 1 2 2 + ( 5 r n − 1 6 ) 2 1 2 r n = 1 4 4 + 2 5 r n 2 − 1 6 0 r n + 2 5 6 1 2 r n = 2 5 r n 2 − 1 6 0 r n + 4 0 0 1 2 r n .
We cannot further simplify this beyond a trivial rationalization, and the recursion is already in the desired form, so we find that a + b + c + d = 1 2 + 2 5 + 1 6 0 + 4 0 0 = 5 9 7 .