Sequential limit

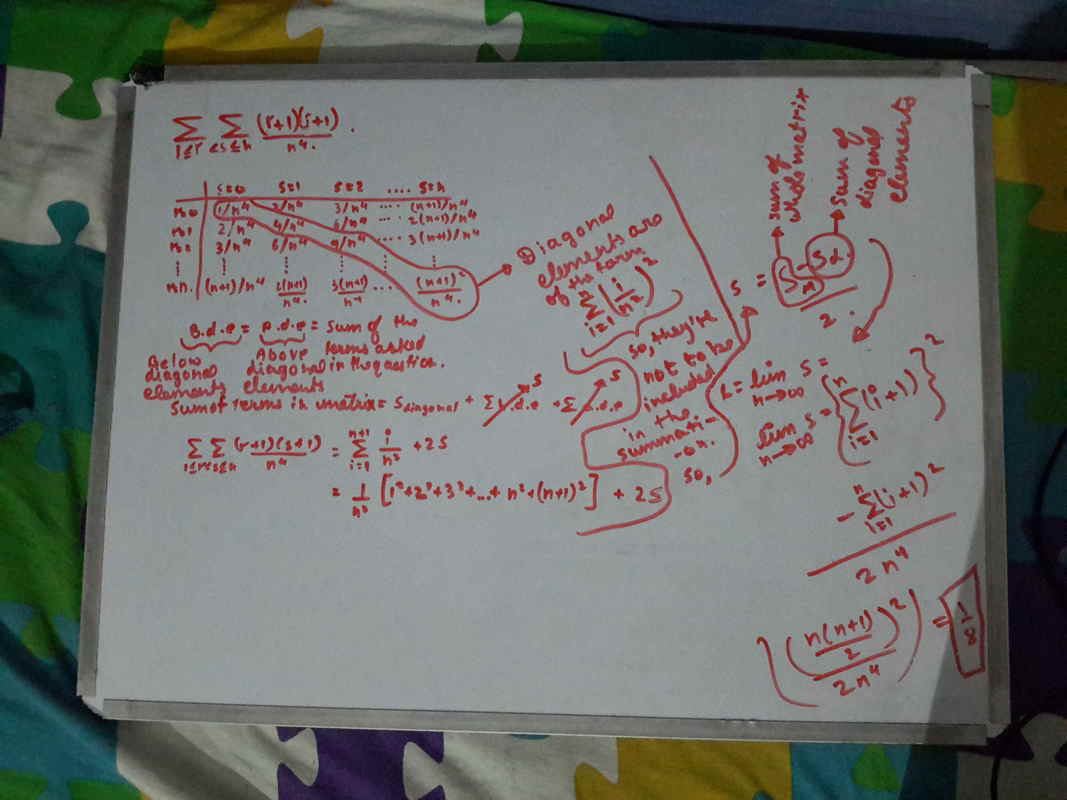
Let our required Limit as " L " . Also Consider an $n\times n$ matrix , Such that ${ a }_{ ij }$ represent element of $i$ th row and $j$ th column. Also let ${ a }_{ ij }=\left( i+1 \right) \left( j+1 \right)$ .

Again let, $\displaystyle{{ S }_{ 1 }=\sum _{ i>j }^{ n }{ { a }_{ ij } } \equiv \sum _{ i>j }^{ n }{ \left( i+1 \right) \left( j+1 \right) } \\ { S }_{ 2 }=\sum _{ i<j }^{ n }{ { a }_{ ij } } \equiv \sum _{ i<j }^{ n }{ \left( i+1 \right) \left( j+1 \right) } \\ { S }_{ 3 }=\sum _{ i=j }^{ n }{ { a }_{ ij } } =\sum _{ i=1 }^{ n }{ { a }_{ ii } } \equiv \sum _{ i=j }^{ n }{ \left( i+1 \right) \left( j+1 \right) } \equiv \sum _{ i=1 }^{ n }{ { \left( i+1 \right) }^{ 2 } } \\ S={ S }_{ 1 }+{ S }_{ 2 }+{ S }_{ 3 }=\sum _{ i=1 }^{ n }{ \sum _{ j=1 }^{ n }{ \left( i+1 \right) \left( j+1 \right) } } \equiv { \left( \sum _{ i=1 }^{ n }{ { \left( i+1 \right) } } \right) }^{ 2 }}$

So Our Target is to calculate ${ S }_{ 2 }=?$ , But Since due to symmetrical distribution in matrix , ${ S }_{ 2 }={ S }_{ 1 }\equiv \cfrac { S-{ S }_{ 3 } }{ 2 }$ .

$\displaystyle{L=\lim _{ n\rightarrow \infty }{ { S }_{ 2 } } =\lim _{ n\rightarrow \infty }{ \left( \cfrac { { \left( \sum _{ i=1 }^{ n }{ { \left( i+1 \right) } } \right) }^{ 2 }-\sum _{ i=1 }^{ n }{ { \left( i+1 \right) }^{ 2 } } }{ 2{ n }^{ 4 } } \right) } \\ L=\lim _{ n\rightarrow \infty }{ \left( \cfrac { { \left( \sum _{ i=1 }^{ n }{ { \left( i+1 \right) } } \right) }^{ 2 } }{ 2{ n }^{ 4 } } -0 \right) } =\lim _{ n\rightarrow \infty }{ \left( \cfrac { { { \left( \cfrac { n(n+1) }{ 2 } \right) }^{ 2 } } }{ 2{ n }^{ 4 } } \right) } \\ \boxed { L=\cfrac { 1 }{ 8 } } \\ }$

Here is my approach to this problem