Sequencing The Digits

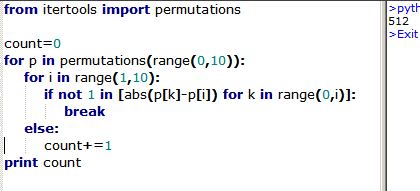
The enumeration of permissible sequences is relatively simple if we classify them according to the position of the digit 0 in the sequence:

(1) There is only one permissible sequence with 0 in the first position: (0,1,2,3,4,5,6,7,8,9).

(2) There is also only one permissible sequence with 0 in the second position: (1,0,2,3,4,5,6,7,8,9).

(3) There are two permissible sequences with 0 in the third position: (1,2,0,3,4,5,6,7,8,9) and (2,1,0,3,4,5,6,7,8,9).

(4) There are four permissible sequences with 0 in the fourth position: (1,2,3,0,4,5,6,7,8,9), (2,1,3,0,4,5,6,7,8,9), (2,3,1,0,4,5,6,7,8,9) and (3,2,1,0,4,5,6,7,8,9).

Now we can see a pattern emerging:

(5) When 0 is in the n-th position (n > 1), the digits to its left are in the set {1,2,...,n-1} and the digits to its right form the subsequence (n,n+1,...,9).

(6) If $(a_1,a_2,\ldots,a_{n-1})$ is a permissible subsequence to the left of 0 when it is in the n-th position, it gives origin to two permissible subsequences when 0 moves to the (n+1)-th position: $(a_1,a_2,\ldots,a_{n-1},n)$ and $(a_1+1,a_2+1,\ldots,a_{n-1}+1,1)$ . Moreover, it is not difficult to prove (but I will not do it here) that, when 0 is in the (n+1)-th position, its left neighbor must be 1 or n. Therefore, that process generates all permissible subsequences when 0 moves from the n-th to the (n+1)-th position.

It follows from the observations above that, if $f(n)$ is the number of permissible sequences with 0 in the n-th position, then $f(1) = f(2) = 1$ and $f(n+1) = 2f(n)$ for $n>1$ . Therefore, the total number of permissible sequences is $f(1) + f(2) + \ldots + f(10) = 1 + 1 + 2 + 4 + \ldots + 2^{8} = \boxed{512}\,$ .