Series on trot
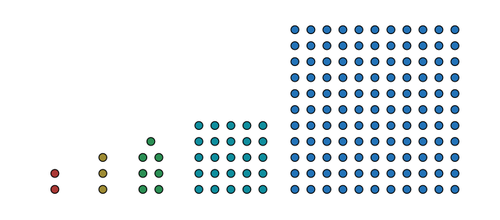 What comes next in this series:
What comes next in this series:
2, 3, 7, 25, 121, __
The answer is 721.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
12 solutions
2 x 2 - 1 = 3 3 x 3 - 2 = 7 7 x 4 - 3 = 25 25 x 5 - 4 = 121 121 x 6 - 5 = 721
Log in to reply
how do you explain the first term of this pattern using the above method? 2x1-0?
Very misleading visual of dots.. :-( These kinds of problems are becoming more and more harder to solve. One can come up with any sort of contorted sequence of numbers and attribute arbitrary logic to it, and ask that it be connected using a formula. :-(
Good one, though.
Log in to reply
Yes, but the arbitrary logic is correct, and the idea is to learn to understand it an to recognize these arbitrary patterns in every sort of contorted number sequence.
1x1+1= 2 not 1
2 2 3 3 7 4 2 5 5 1 2 1 6 ↓ ( x ) 7 2 1 7 ← ↩ ( − ) . . . . ( 1 2 1 × 6 ) − 5 = 7 2 1
good solution
but 1x1+1=2 and 2x1+1=3
Is 1×1+1=1????? Is not rather 2
NO, 1x1+1= 2 !!
great solutions by all
AAccckkk! I was doing 2x2-1......
1x1+1=1 ????
I couldnot recognize the pattern
Factorial of natural nos+1
A038507 OEIS
2!+1=3
3!+1=7
4!+1=25
5!+1=121
6!+1=721
Idea of factorial numbers isvery good
good solution
It can be solved recursively as well. Through induction it can be proved that a n = ( a n − 1 ) n − ( n − 1 ) ∀ n ∈ N such that n ≥ 2 is equal to f ( n ) = n ! + 1 :
let a 1 = 2
We prove the base case by showing this relation holds true for n = 2 :
a 2 = a 1 ∗ 2 − ( 2 − 1 ) f ( 2 ) = 2 ! + 1
a 2 = 3 f ( 2 ) = 3
Now we assume k is true for all k such that:
a k = ( a k − 1 ) k − ( k − 1 ) f ( k ) = k ! + 1
We can rearrange the terms in the a k recursive formula to give:
a k = ( a k − 1 − 1 ) k + 1
Since we are trying to prove the equivalence of the two formulas, we can clearly write:
( a k − 1 − 1 ) k + 1 = k ! + 1
We will try to prove this is true for k+1. We make cancel the 1 term on both sides of the equation and it will be enough to prove the equivalence of the formulas by proving a k = k ! + 1 , as we assumed earlier:
( a k − 1 ) ( k + 1 ) = ( k + 1 ) !
( a k − 1 ) ( k + 1 ) = ( k + 1 ) ( k ) ! divide by (k+1)
a k − 1 = k !
a k = k ! + 1
...
I thought this was a fun exercise in math induction more than anything, but the answer still remains. The 6th term of this recursive formula is 721 .
2!+1=3 3!+1=7 4!+1=25 5!+1=121 6!+1=721
The series goes as
1!+1
2!+1
3!+1
4!+1
5!+1
and then 6!+1 which is 721
3=2×2-1=2×2-(2-1)
7=3×3-2=3×3-(3-1)
25=7×4-3=7×4-(4-1)
121=25×5-4=25×5-(5-1)
121×6-5=721
(previous number)n-m , n=2,3,4,5,6,...m=1,2,3,4,5,... 2(2)-1=3 3(3)-2=7 7(4)-3=25 25(5)-4=121 121(6)-5=721
Dots are cleverly misleading. :)
My own arithmetic is poor, consequently I resort to Python. This was my last experiment.
>>> for i in range(1,7):
... factorial(i)+1
...
2
3
7
25
121
721
It this serie: (n! +1) n=1 -> (1+1) = 2. n=2 -> (2+1) = 3. n=3 -> (6+1) = 7. n=4 -> (24 +1) =25. n=5 -> (120 +1) = 121. n=6 -> (720 +1) = 721 ... ...
2-3=1=(1*0!^(1/2))^2
7-3=4=(2*1!^(1/2))^2
25-7=18=(3*(2!^(1/2)))^2
121-25=96=(4*(3!^(1/2)))^2
x-121=(5*(4!^(1/2)))^2
x=721
a(5)=(5+1)!+1;a(5)=6!+1;a(5)=720+1;a(5)=721.i take up series starting from 3 and found the 5th term.
1x1+1=1
2x1+1=2
3x2x1+1=7
4x3x2x1+1=25 5x4x3x2x1+1=121
6x5x4x3x2x1+1=721