Seriously, Who Developed The Mod Function?

Relevant wiki: Absolute Value Problem Solving - Intermediate

Substituting $x$ by $-x$ returns the same equation. Similarly substituting $y$ by $-y$ also returns the same equation. Therefore the graph represented by this equation is symmetrical about both the x and y axes and the length of the graph in all the quadrants is the same.

$\therefore$ The length of graph $=$ $4 \times$ the length of graph in the first quadrant.

In the first quadrant, $x>0$ and $y>0$ , $\therefore$ the equation reduces to $||x-a|-b|+||y-a|-b|=1$

Now, if we shift the origin to $(a,a)$ , the equation becomes $||x|-b|+||y|-b|=1$ , which is again symmetrical about both the axes. Therefore, the graph in the first quadrant can further be divided into 4 symmetric regions by the lines $x=a$ and $y=a$ :

• Region A $a \leqslant x$ , $a \leqslant y$

• Region B $0 \leqslant x \leqslant a$ , $a \leqslant y$

• Region C $0 \leqslant x \leqslant a$ , $0 \leqslant y \leqslant a$

• Region D $a \leqslant x$ , $0 \leqslant y \leqslant a$

Now, in the region A, $a \leqslant x$ , $a \leqslant y$ , therefore the equation becomes $|x-(a+b)|+|y-(a+b)|=1$ whose graph is a square congruent to $|x|+|y|=1$ but centered at $(a+b,a+b$ and has side $\sqrt{2}$ and vertices $(a+b,a+b+1)$ , $(a+b,a+b-1)$ , $(a+b+1,a+b)$ and $(a+b-1,a+b)$ . Maximum x-coordinate(and also y) of the square = $a+b+1$ , Minimum x-coordinate(and also y) of the square = $a+b-1$ .

If any portion of the graph in the region A lies outside the region $x \leqslant 2a$ , $y \leqslant 2a$ then its reflection in the regions B,C or D might not completely lie in the first quadrant. Therefore, there can be 3 cases :

1- The square completely lies inside $x \leqslant 2a$ , $y \leqslant 2a$ , i.e. all corners of the square are on or inside $x=2a$ or $y=2a$ or $a+b+1\leqslant 2a$ (Max x and y coordinate of the square are less than $2a$ .)

Then the graphs in regions B, C and D will be congruent to the graph in the region A.

$\therefore$ The length of graph $= 4 \times$ the length of graph in the first quadrant.

$= 4^2 \times$ the length of graph in the region A $= 4^2 \times 4 \times$ side of square $|x-(a+b)|+|y-(a+b)|=1$ $= 4^3\sqrt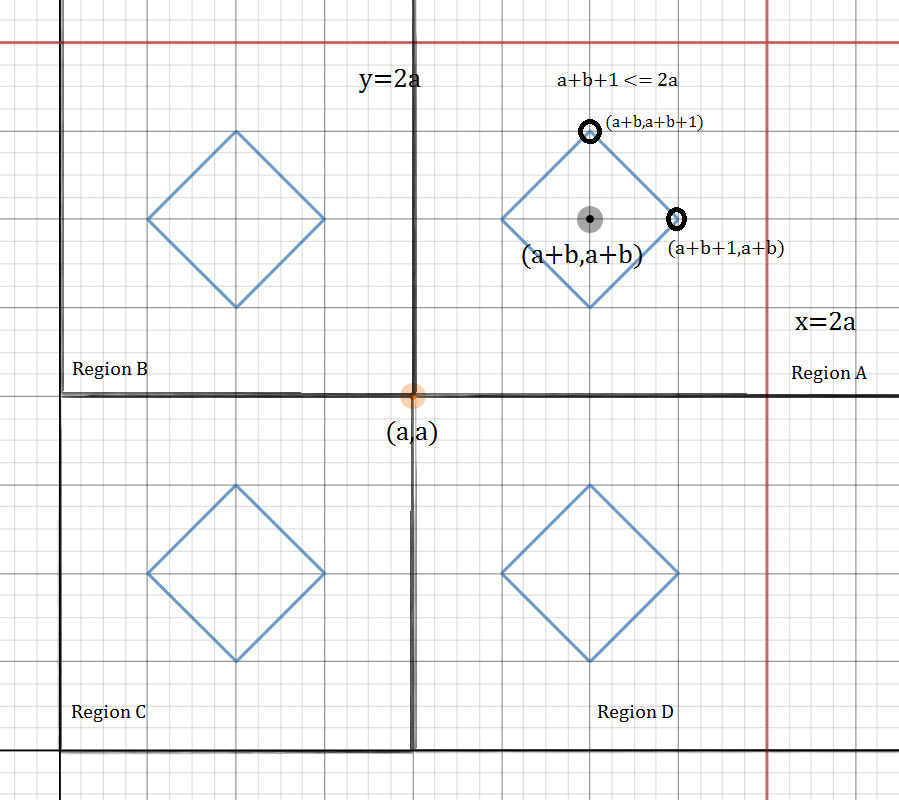{2} = 64\sqrt{2}$

2- The square partially lies inside $x \leqslant 2a$ , $y \leqslant 2a$ i.e. $a+b-1\leqslant 2a$ and $a+b+1\geqslant 2a$ or $a+b = 2a$ (Min x and y coordinate of the square are less than $2a$ but max x and y coordinate of the square are greater than $2a$ .)

Then only two sides of the square in region A will be reflected in region B and D and only one side will be reflected in region C.

$\therefore$ The length of graph $= 4 \times$ the length of graph in the first quadrant.

$= 4 \times$ ( $4$ (no. of sides of square in region A) + $2$ (in region B) + $1$ (in region C) + $2$ (in region C)) $\times$ side of square

$=36\s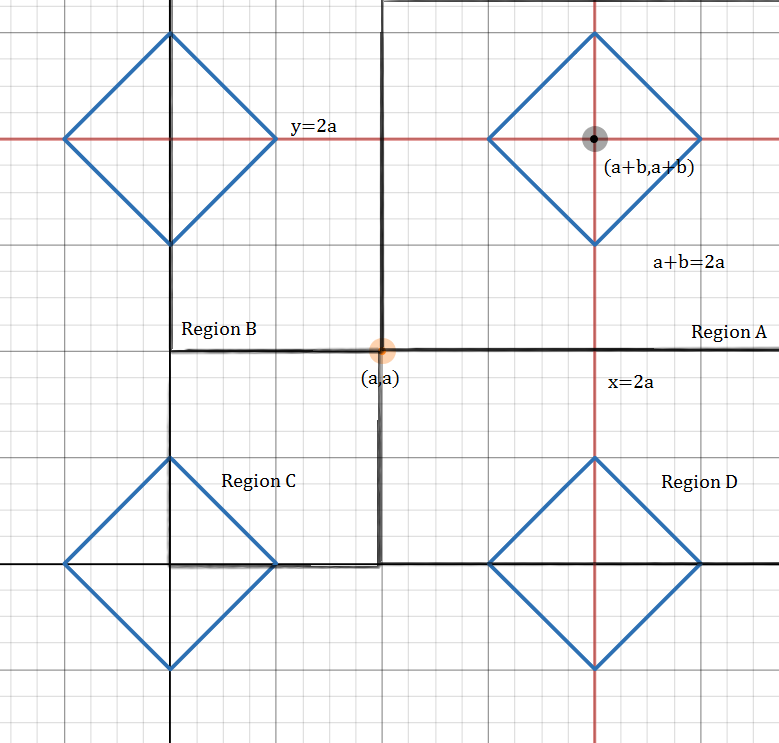qrt{2}$

3- The square completely lies outside $x \leqslant 2a$ , $y \leqslant 2a$ , i.e. all corners of the square are on or outside $x=2a$ or $y=2a$ or $a+b-1\geqslant 2a$ (Min x and y coordinate of the square are greater than $2a$ .)

Then no portion of the graph in region A will be reflected in region B, C or D.

$\therefore$ The length of graph $= 4 \times$ the length of graph in the first quadrant.

$= 4 \times$ the length of graph in the region A $= 4 \times 4 \times$ side of square $|x-(a+b)|+|y-(a+b)|=1$ $= 4^2\sqrt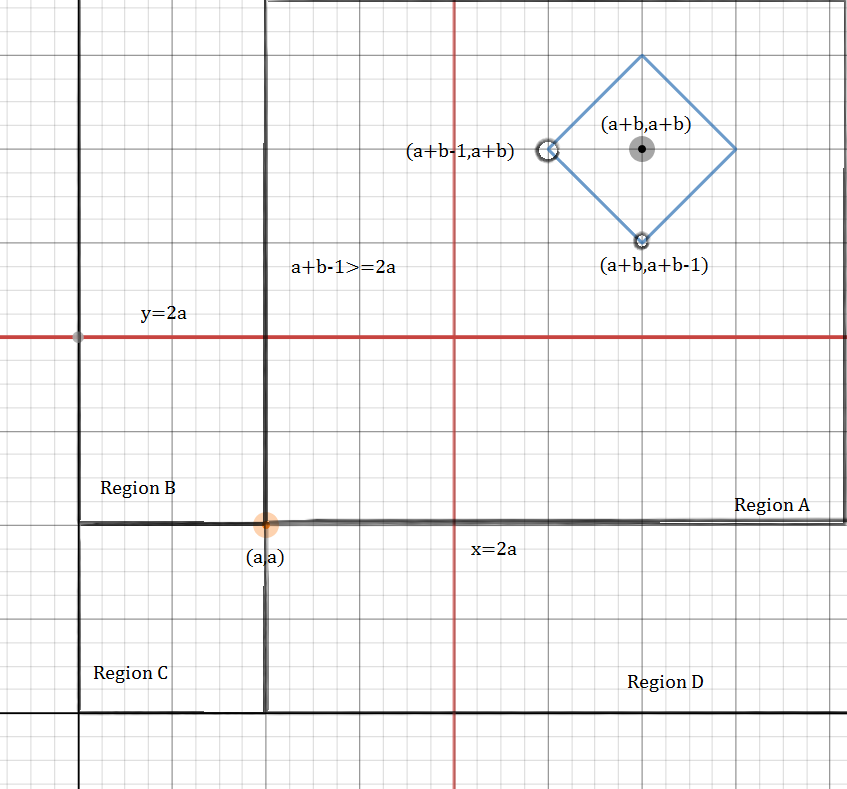{2} = 16\sqrt{2}$

Thus the length of graph can take 3 different values , i.e. $n=3$ .

S $=$ Sum of all possible lengths $= 64\sqrt{2} + 36\sqrt{2} + 16\sqrt{2} = 116\sqrt{2}$

Answer $= \frac{\frac{S}{\sqrt{2}}+1}{n}$

$= \frac{116+1}{3}\ = 39$