Seven Circles in a Hexagon
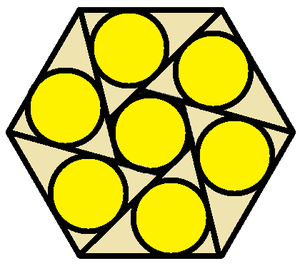
Seven identical circles are arranged symmetrically inside a regular hexagon with a side length of 1 as shown in the figure above.
If the radius of each of these circles is given by r = c a − b , where a , b , and c are integers with a and b being square-free, find a + b + c .
The answer is 26.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
sin , not sin − 1 , in your formula...
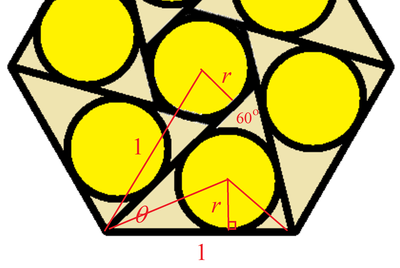
Let the radius of the circle be r . Let us consider one of the six triangles and I have chosen the bottom one as shown ( @David Vreken , if you have used thiner lines, it would be easy for me to reuse the figure). We note the top angle of the triangle is always 6 0 ∘ . Let the smaller base angle be θ . Then the other base angle is 1 2 0 ∘ − θ . For the length of the bottom side of the hexagon, we have:
r cot 2 θ + r cot ( 6 0 ∘ − 2 θ ) = 1
Now consider the radius of the center circle. We note that r = sin ( 6 0 ∘ − θ ) . Substitute into the equation above:
sin ( 6 0 ∘ − θ ) ( cot 2 θ + cot ( 6 0 ∘ − 2 θ ) ) ( 2 3 cos θ − 2 1 sin θ ) ( tan 2 θ 1 + cot ( 6 0 ∘ − 2 θ ) ) ( 3 ⋅ 1 + t 2 1 − t 2 − 1 + t 2 2 t ) ( t 1 + 3 − t 1 + 3 t ) ( 1 + t 2 3 − 2 t − 3 t 2 ) ( 3 t − t 2 3 ( 1 + t 2 ) ) 3 − 2 3 t − 3 t 2 ⟹ t 2 + 4 3 t − 3 ⟹ t = 1 = 1 = 2 = 2 = 2 3 t − 2 t 2 = 0 = 1 5 − 1 2 Let t = tan 2 θ
Then we have:
r = 2 ( 1 + t 2 ) 3 − 2 t − 3 t 2 = 2 ( 1 + 2 7 − 1 2 5 ) 3 − 2 ( 1 5 − 2 3 ) − 3 ( 2 7 − 1 2 5 ) = 8 ( 7 − 3 5 ) 1 0 1 5 − 2 2 3 = 4 ( 7 − 3 5 ) ( 7 + 3 5 ) ( 5 1 5 − 1 1 3 ) ( 7 + 3 5 ) = 8 1 5 − 3
Therefore a + b + c = 1 5 + 3 + 8 = 2 6 .
The six triangles formed have sidelengths 1 , a , b , where (say) a < b , and the angle between the sides of length a , b is 6 0 ∘ . The area of one of these triangles is therefore Δ = 2 1 a b sin 6 0 = 4 3 a b
and the semiperimeter is 1 + a + b . Hence the inradius is r = 2 3 ⋅ 1 + a + b a b
Also, by the cosine rule, 1 = a 2 + b 2 − a b
The central hexagon has sidelength a − b ; so the radius of the central circle is 2 3 ( b − a ) .
Equating these radii, we have to solve 2 3 ( b − a ) = 2 3 ⋅ 1 + a + b a b
and 1 = a 2 + b 2 − a b
These are messy but not hard to solve; we find a = 4 1 ( 1 + 5 ) and b = 2 1 5 , from which we find r = 8 1 5 − 3
giving the answer 2 6 .
The length of each side of the inner hexagon is 4 5 − 1
Radius of each circle is
2 3 × 4 5 − 1 = 8 1 5 − 3
So, a = 1 5 , b = 3 , c = 8 , and a + b + c = 2 6 .
Do you have the proof for the first line?
Log in to reply
Proof of this is elaborated by Thanos Petropoulos.
x(1+2√(1-x²)) = √3/2-2x²/√3 Have to make WA to churn out the answer though.
Log in to reply
Repeatedly squaring can show that we can get the answer without computer assistance.
This problem (as well as this one ) is a variation of of “Suzuki’s problem of four congruent incircles in an equilateral triangle” . In this paper, the following generalisation theorem is stated and proven:
In our case, a 0 = 1 and n = 6 , so for the side of the inner hexagon we get 1 = a i ( 1 + 1 + ( sin 6 π ) − 2 ) ⇒ a i = 1 + 1 + ( 2 1 ) − 2 1 = 1 + 5 1 The radius r of the inscribed circle is the apothem of the regular hexagon, thus we have r = 2 3 a i = 2 3 ⋅ 1 + 5 1 = 8 1 5 − 3 For the answer, a = 1 5 , b = 3 , c = 8 , hence a + b + c = 2 6 .